Sätze in der Geometrie
Satz des Thales
Liegt die längste Seite eines Dreiecks genau auf dem Durchmesser eines Kreises und der gegenüberliegende Punkt des Dreiecks auf der Kreislinie, dann ist das Dreieck rechtwinklig.
Strahlensätze
Um unbekannte Strecken in einem Dreieck zu bestimmen kann man, wenn man ein ähnliches Dreieck kennt, sich mit den Strahlensätzen behelfen.
Diese Sätze geben Verhältnisse an, die auf einer maßstabsgetreuen Streckung der Figur beruhen.
Es gibt zwei Strahlensätze:
Versuch es selbst:
erster Strahlensatz
Da die Geraden g und g' zueinander parallel sind (g || g'), teilen sie die beiden bekannten Schenkel in gleichen Verhältnissen. Daher gilt die Formel im Bild.
zweiter Strahlensatz
Satz des Pythagoras
In einem rechtwinkligen Dreieck gilt: die Quadrate über den Katheten sind in der Summe gleich groß wie das Quadrat über der Hypotenuse
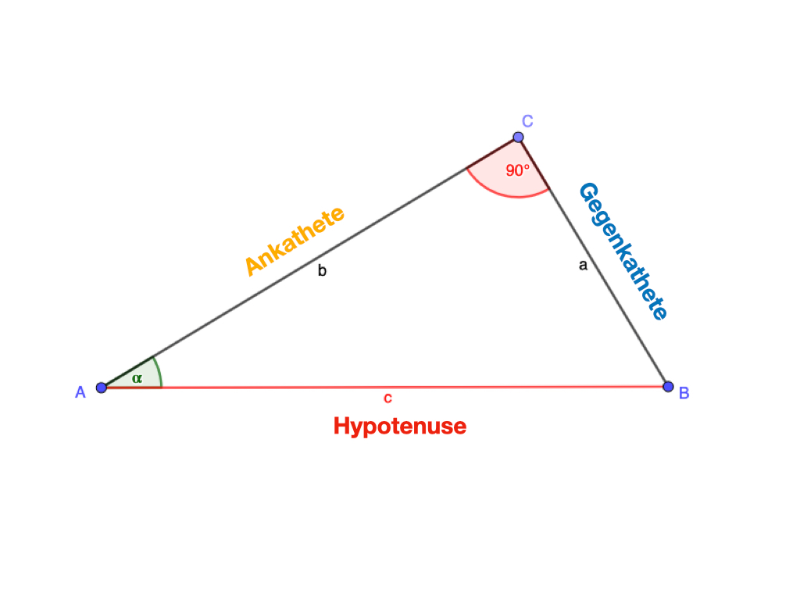
Im rechtwinkligen Dreieck haben die Seiten besondere Begriffe:
Katheten: so bezeichnet man die Seiten, die am rechten Winkel anliegen.
Ankathete: Bezeichnet die Seite, die an einem bekannten Winkel (zusätzlich zum rechten Winkel) anliegt. (In unserem Beispiel ist bekannt)
Gegenkathete: Bezeichnet die Seite, die nicht an einem bekannten Winkel (zusätzlich zum rechten Winkel) anliegt. Der Winkel liegt also gegenüber der Seite.
Hypotenuse: bezeichnet die längste Seite im Dreieck. Sie liegt immer gegenüber dem rechten Winkel.
Höhensatz
Ist ein Dreieck rechtwinklig mit γ = 90°, dann gilt:
Kathetensatz
Ist ein Dreieck rechtwinklig mit γ = 90°, dann gilt: und
Pythagoras im Körper
Um die Raumdiagonale eines Quaders zu berechnen ist das Wissen um den Pythagoras sehr hilfreich. Da es sich beim Quader um einen dreidimensionalen Körper handelt, bei dem alle Seiten im rechten Winkel zueinander angeordnet sind, gilt folgende Formel:
(im Würfel gilt: )
Pythagoras im Quader (Hinweis: e ist die Hypotenuse des Dreiecks ABC, also die Diagonale der Grundfläche))
Pythagoras in der Pyramide
Satz vom Umfangswinkel
Wenn in einem Kreis ein Winkel eine Sehne aufspannt, dann ist dieser doppelt so groß wie ein Winkel von den Sehnenpunkten zur Umfangslinie des Kreises.
Es gilt: