Euklids Algorithmus und chinesischer Restsatz
In der Kryptografie ist die Berechnung des größten gemeinsamen Teilers (ggt) eine häufige Aufgabe.
Der euklidische Algorithmus
löst diese Aufgabe effizient, allerdings erfordert er die Berechnung der mod-Funktion, also im Prinzip eine Division mit Rest. Mit dem steinschen Algorithmus [Stein 67] lässt sich der größte gemeinsame Teiler ohne Divisionen berechnen. Der steinsche Algorithmus benutzt lediglich Division durch 2; diese lässt sich durch eine Schiebeoperation (js: <<) effizient realisieren.
https://www.inf.hs-flensburg.de/lang/krypto/algo/ggt-stein-algorithmus.htm
Klick Textblock to run the described code (js)
CAS Iteration steps controlled by slider n
GCD - ggb function call
Für die Berechnung im CAS muss n angepasst/eingestellt werden, der Euklidische Algorithmus in Zeile (2)
dargestellt durch Igcd muss in der 2.Spalte mit einer 0 abschließen!
Erweiterter euklidischer Algorithmus
(Lemma von Bézout)
Seien a, b 
0.
Der größte gemeinsame Teiler ggt(a, b) lässt sich als ganzzahlige Linearkombination von a und b darstellen:
ggt(a, b) = u·a + v·b mit u, v 
Die Darstellung ist nicht eindeutig; die Gleichung wird durch verschiedene Zahlenpaare u, v erfüllt.
Der erweiterte euklidische Algorithmus berechnet zusätzlich noch eine Darstellung von ggt(a, b) als ganzzahlige Linearkombination von a und b.
Er berechnet den größten gemeinsamen Teiler g zweier Zahlen a und b und zusätzlich die Koeffizienten u und v einer Darstellung von g als ganzzahlige Linearkombination.
Recursion
function extgcd(a, b) {
if (b == 0) {
return [a, 1, 0]
} else {
guv = extgcd(b, a % b);
return [guv[0], guv[2], guv[1] - parseInt(a / b) * guv[2]]
}
}
Iteration
0.
Der größte gemeinsame Teiler ggt(a, b) lässt sich als ganzzahlige Linearkombination von a und b darstellen:
ggt(a, b) = u·a + v·b mit u, v
Die Darstellung ist nicht eindeutig; die Gleichung wird durch verschiedene Zahlenpaare u, v erfüllt.
Der erweiterte euklidische Algorithmus berechnet zusätzlich noch eine Darstellung von ggt(a, b) als ganzzahlige Linearkombination von a und b.
Er berechnet den größten gemeinsamen Teiler g zweier Zahlen a und b und zusätzlich die Koeffizienten u und v einer Darstellung von g als ganzzahlige Linearkombination.
Recursion
function extgcd(a, b) {
if (b == 0) {
return [a, 1, 0]
} else {
guv = extgcd(b, a % b);
return [guv[0], guv[2], guv[1] - parseInt(a / b) * guv[2]]
}
}
Iteration
function extgcd(a, b) {
a,b, u = 1; v = 0; s = 0; t = 1;
do {
q = parseInt(a / b);
tmp = b; b = a - q * b; a = tmp;
tmp = s; s = u - q * s; u = tmp;
tmp = t; t = v - q * t; v = tmp;
} while (b != 0)
return [a, u, v]
};
ab = extgcd(99, 78);
[3,-11,14]
CAS (2) per Iterationlist (a,b,u,v,s,t):
n einstellen, so das Divisor 2.Spalte 0 wird!(erweiterter) euklidischer Algorithmus für größten gemeinsamen Teilers zweier Zahlen
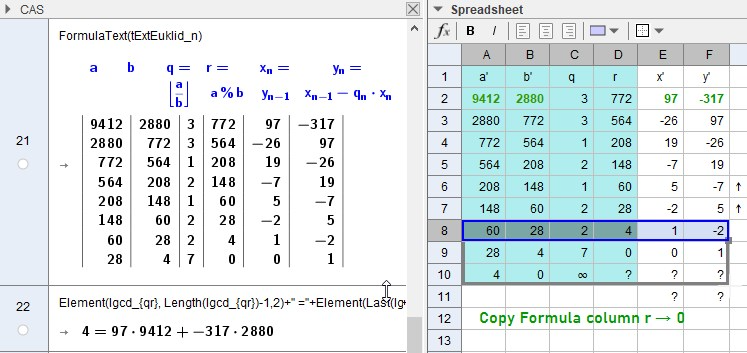
Extgcd(99,78) im SpreadSheet Algorithmus
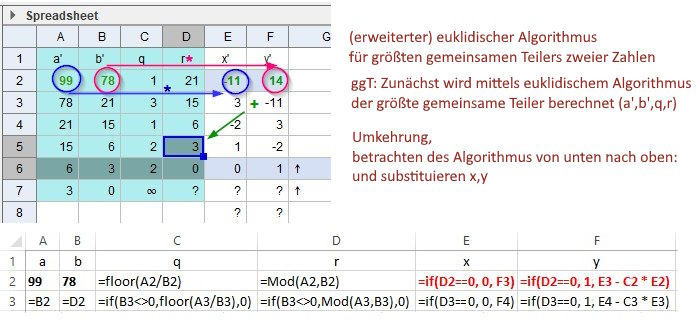
Erweiterter Euklid'scher Algorithmus im CAS
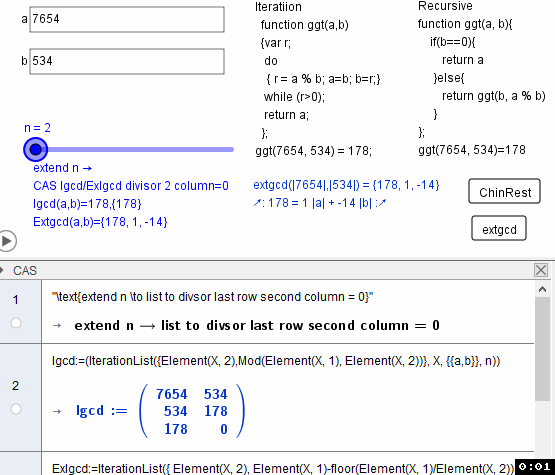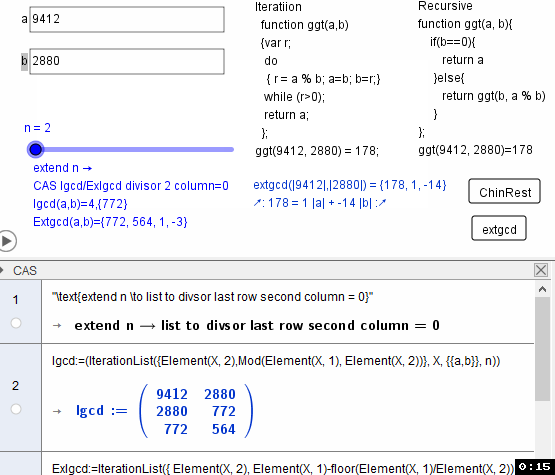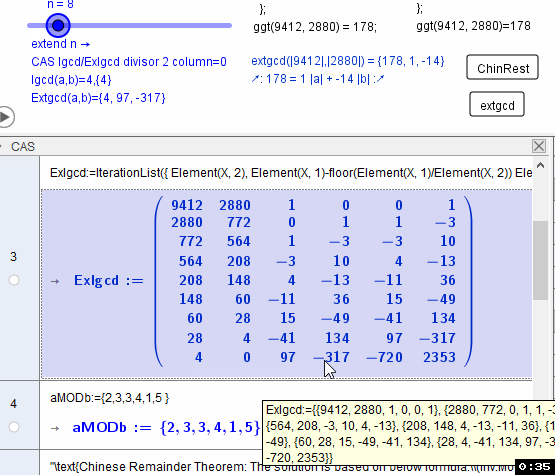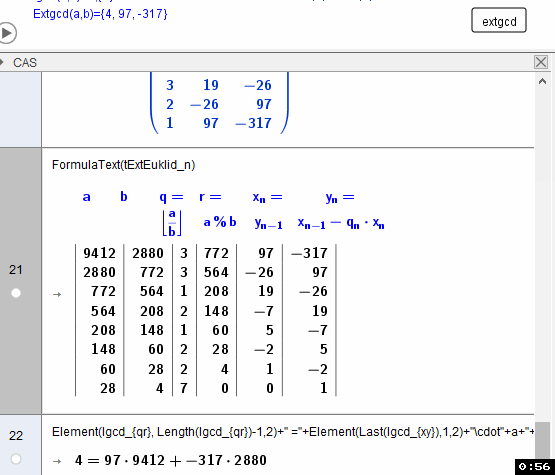
ExtGCD(9412,2880)
Chinesischer Restsatz / Chinese remainder theorem(CRT)
Kryptografie (H.W. Lang Hochschule Flensburg)
https://www.arndt-bruenner.de/mathe/scripts/chinesischerRestsatz.htm
CAS
(3) aMODb:={1,7,5,8,4,9}
x ≡ 1 mod 7
x ≡ 5 mod 8
x ≡ 4 mod 9
chineseRemainder([7,8,9], [1,5,4])
==>[ChinRest]
x ≡ 85 mod 504
[ChinRest]
function chineseRemainder(nn, rr) {
if (nn.length == 1) {
return [nn[0], rr[0]]
} else {
var k = parseInt(nn.length / 2);
var ma = chineseRemainder(nn.slice(0, k), rr.slice(0, k));
var nb = chineseRemainder(nn.slice(k), rr.slice(k));
var guv = extgcd(ma[0], nb[0]);
var x = (nb[1] - ma[1]) * guv[1] % nb[0] * ma[0] + ma[1];
return [ma[0] * nb[0], x]
}
};
[ a x mod n = 1]
function modinv(a, n) {
guv = extgcd(a, n);
var x = guv[1] % n;
if (x < 0) x += n;
return x;
};
CAS step wise
aMODb:={2,3,3,4,1,5 } ===> res mod num
res:=Sequence(aMODb( j),j,1,Length(aMODb),2)
>{2,3,1}
num: Sequence(aMODb(j),j,2,Length(aMODb),2)
>{3,4,5}
prod: Product(num)
>prod:=60
pp:Sequence(1/ num( j),j,1,Length(num)) prod
>pp:={20,15,12}
inv: Flatten(Sequence( Sequence(j (Mod(j*pp(i),num(i))==1),j,0,num(i) -1)\{0} ,i,1,Length(num)))
>inv:={2,3,3}
A naive solution to find minimum x is the solution based on formula
res: remainder, num: modulo, pp: prod/num(i),
inv - moduloinverse x: pp(i)*x mod num(i) = 1 (brutforce test over all mods either way v return of extgcd, v factor of a, v mod n )
xres:= Mod(Sum(res(i)*pp(i)*inv(i) ,i,1,Length(num)) , prod)
>xres:=11
Sequence({xres = res(j),mod,num(j)},j,1,Length(num))
https://www.youtube.com/watch?v=S_Dfw7J9EBE