Lesson 2; Keeping the Equation Balanced
Lesson Overview
Warm Up
What do you notice? What do you wonder?
Ask your self
Lauching the Assignment
Applet Usage/Question
This picture represents a hanger that is balanced because the weight on both sides is the same.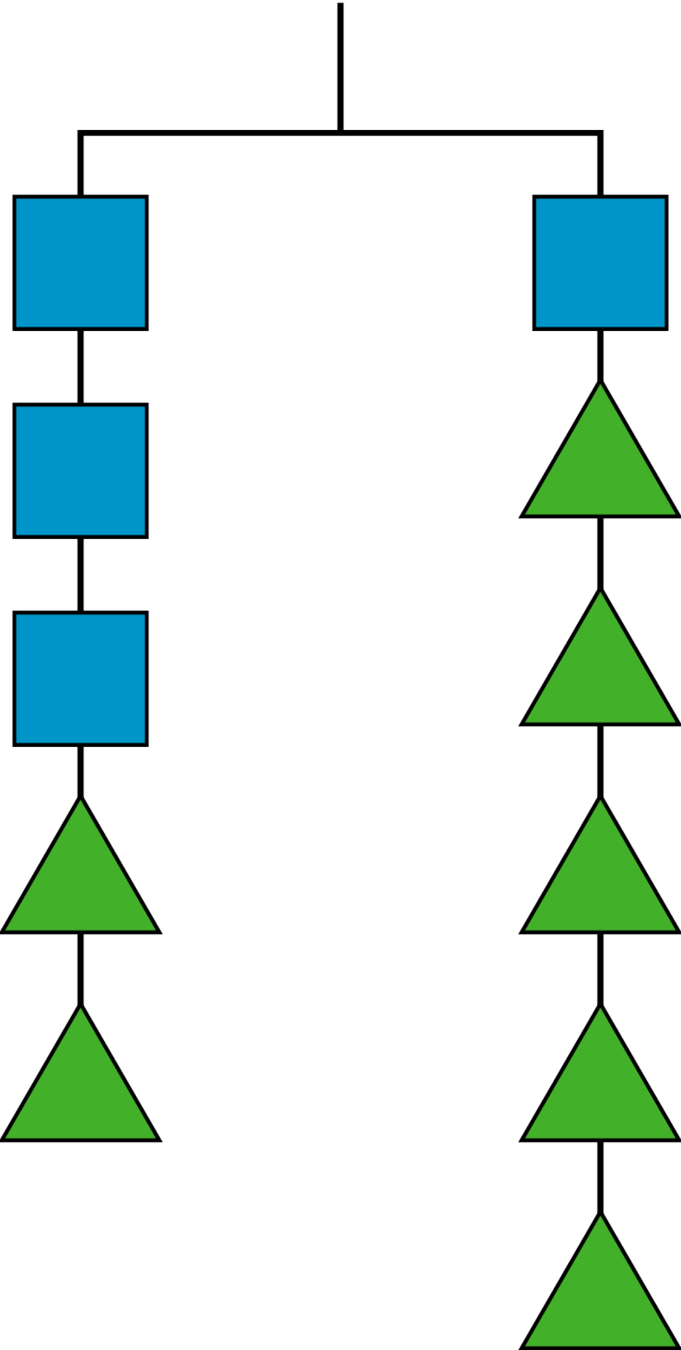
Question 2
Pass
A triangle weighs 3 grams and a circle weighs 6 grams.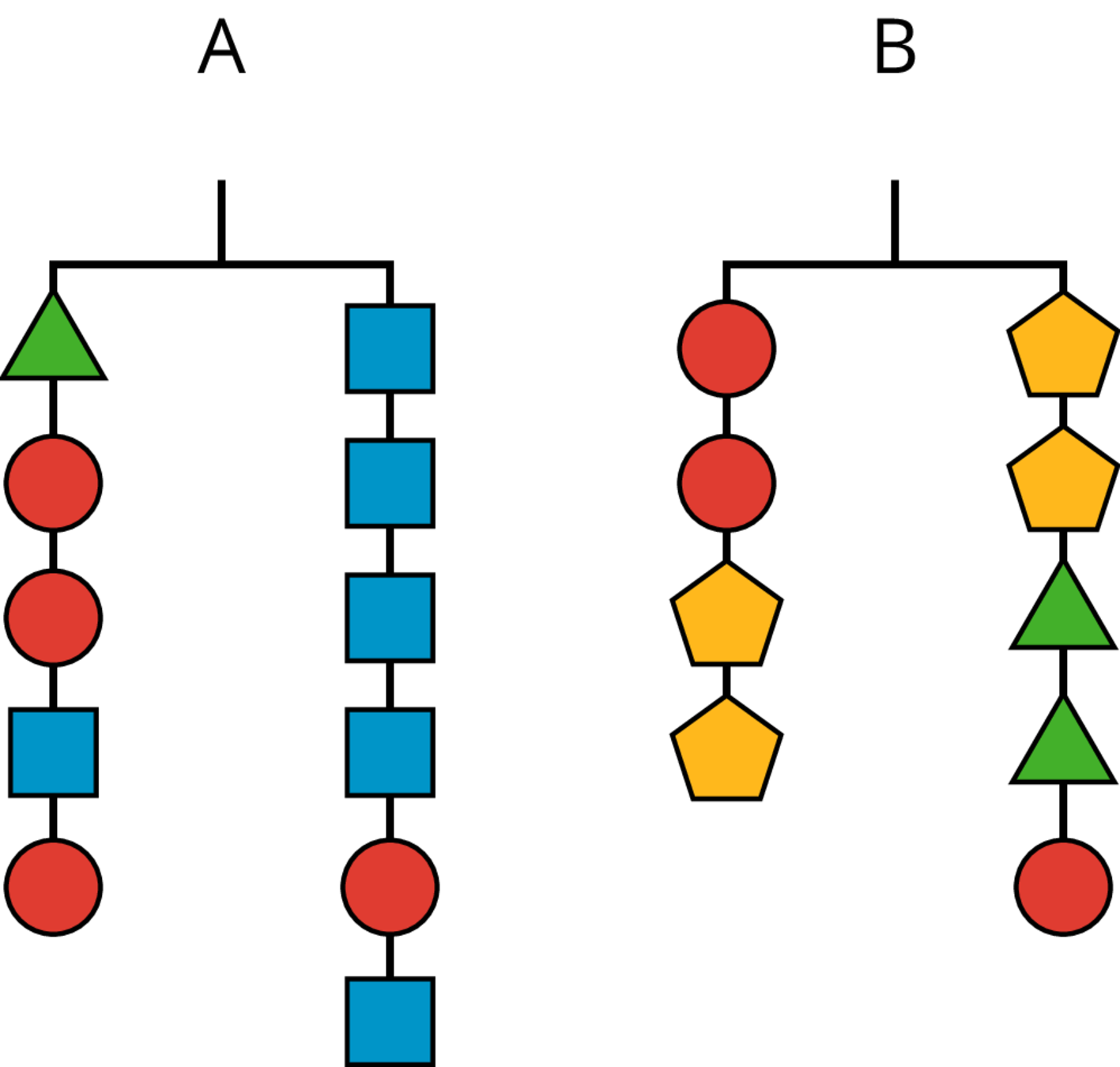
Hey, are you ready for more?
What is the weight of a square on this hanger if a triangle weighs 3 grams?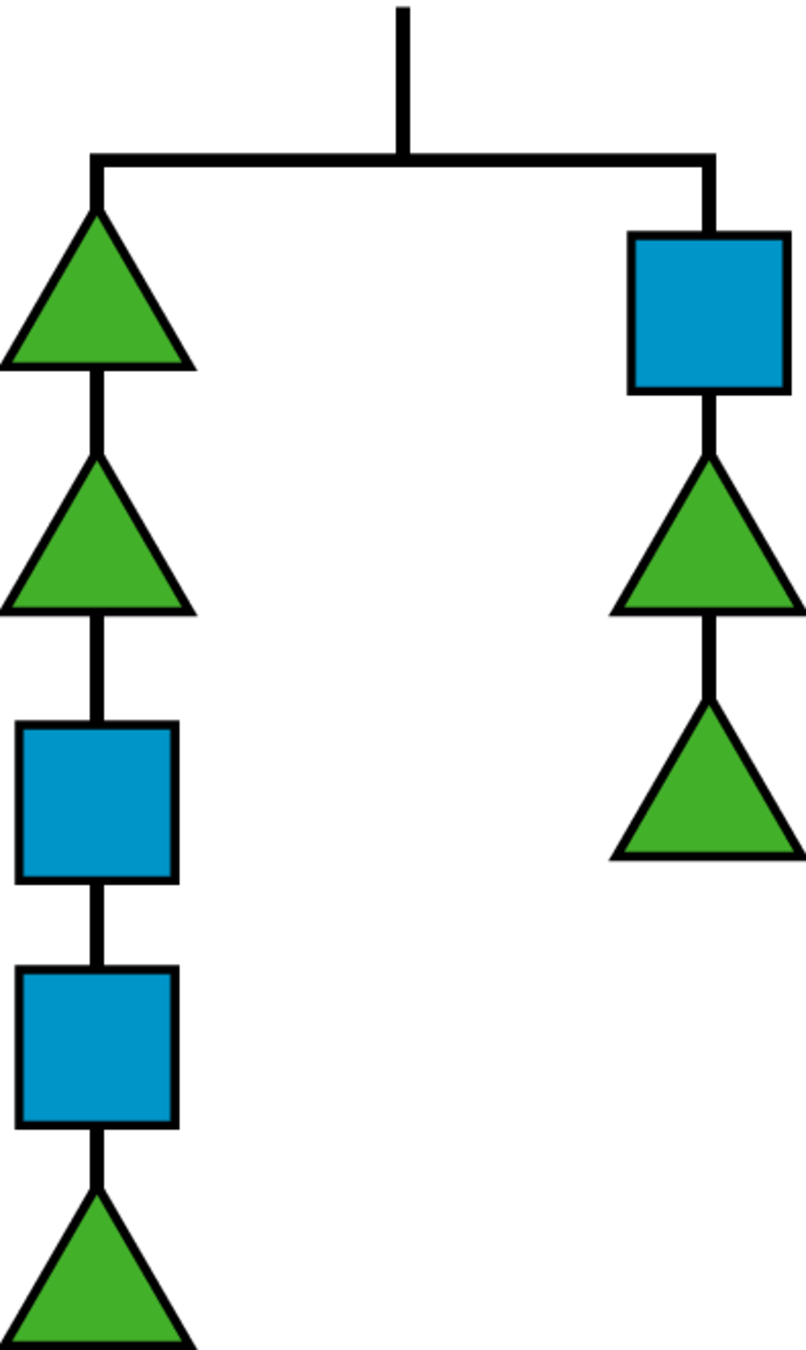
Summary
- Removing an x from each side of the second equation would result in the first equation.
- x=3.75 grams makes both equations true.
- You can subtract 6s from the sides of each equation and they are still both true.
Homework
Here is a hanger that is in balance. We don’t know how much any of its shapes weigh. How could you change the number of shapes on it, but keep it in balance? Describe in words or draw a new diagram.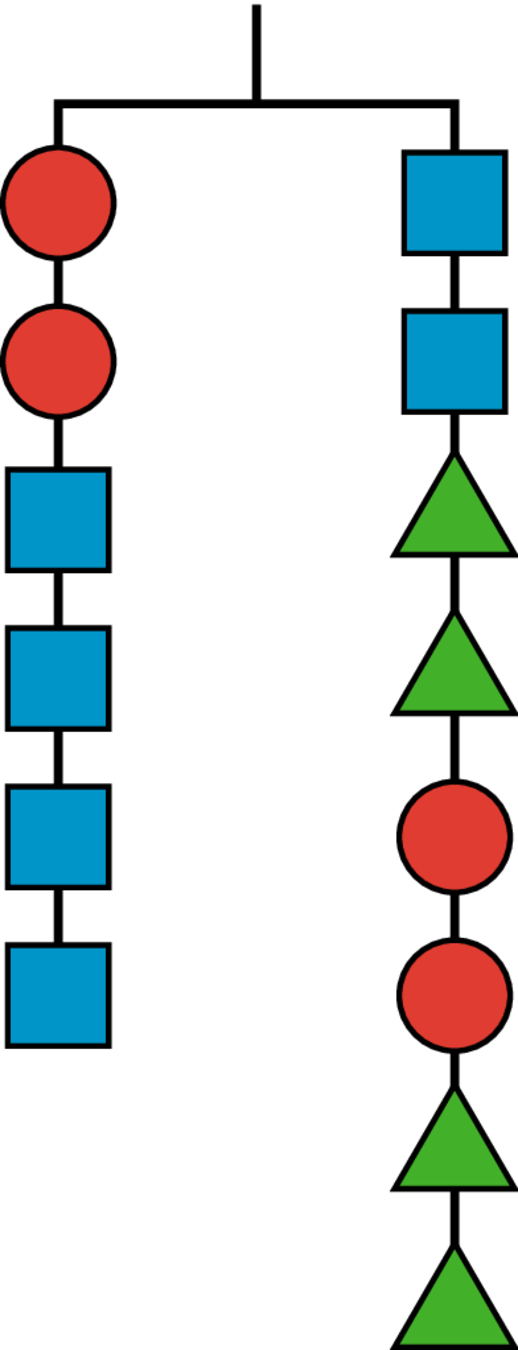
"Summary 2"
- “In the warm-up we wondered why one hanger was slanted, whether there were weights in one blue sock that made it heavier than the other, whether the crooked hanger would straighten out if another sock was added to the other side (add any other pertinent things your students wondered). How would you answer these questions now?”
- “What is an equation? What does the equal sign in an equation tell you?” (An equation is a statement that two expressions have the same value. The equal sign tells you that the expressions on either side must have the same value, however that value is measured—as a count of objects, a measurement like 10 miles or 6 seconds, or numbers without units.)
- “What features do balanced hangers and equations have in common?” (Both representations have sides that are equal in value, even if the actual value of a side is unknown. Each side can contain numbers we do not know in the form of either shapes or variables. Changing the value of one side of a hanger or equations means changing the value of the other side by the same amount.)
- “You saw an example of a hanger where the unknown weight could not be determined. Can you design your own hanger like this one? How would you think about the weights needed on each side?” (If students completed the extension, you might ask them to also design a hanger with no solution.)