Cálculo de alturas inaccesibles
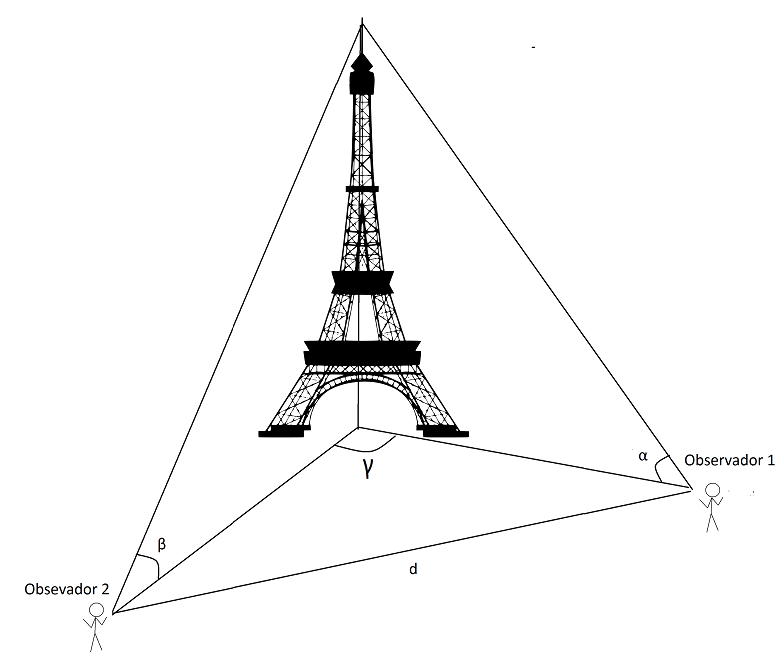
Se presenta la resolución de un problema de la medida de la altura de la torre conociendo los siguientes datos:
- El ángulo desde el que observa la torre el observador 1 ()
- El ángulo desde el que observa la torre el observador 2 ()
- El ángulo con vértice en el pie de la torre que forman ambos observadores ()
- La distancia (d) entre ambos observadores expresadas en las mismas unidades que la altura de la torre que se pretende medir (u)
El programa Geogebra adjuntado modela la situación de manera dinámica fijando la torre en el origen de coordenadas y el observador 1 de manera libre en el eje x. Dado el ángulo , se calcula la altura "provisional" de la torre, a partir de la cual se determina la ubicación del observador 2 para que contemple dicha altura desde su ángulo correspondiente () sobre la recta que determina el ángulo entre ambos observadores (). Ahora imponemos la distancia entre los observadores (d), generando la circunferencia de centro observador 1 y radio d y movemos el observador 1 hasta que la circunferencia contenga al observador 2 determinado, lo cual determina el valor exacto de la altura que pretendemos calcular.
Nota: Se han despreciado las alturas de los observadores y la diferencia de desniveles en las observaciones realizadas, que complica el cálculo, pero el programa se puede reformular para dar cabida a estos parámetros y hacerlo más realista. 