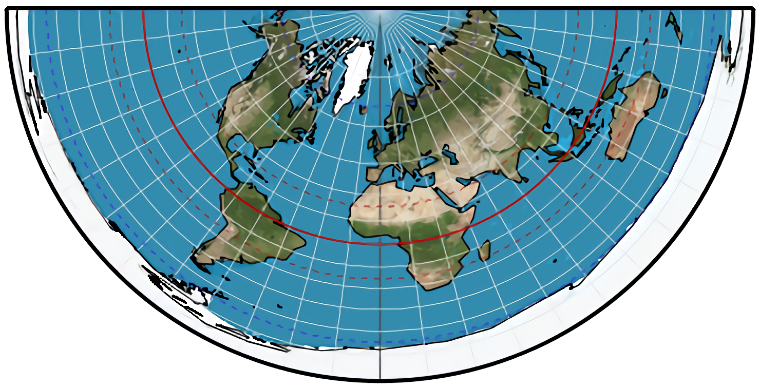
Braunova kuželová projekce
Braunova kuželová projekce je přímá projekce na tečnou kuželovou plochu ke sféře. Zvolíme tečnou rovnoběžku o 30° severní nebo jižní zeměpisné šířky a okolo ní opšíšeme sféře tečnou kuželovou plochu. Body sféry na tuto plochu promítneme z pólu na opačné polokouli než volíme tečnou rovnoběžku.
Zobrazení není ani úhlojevné ani plochojevné, ale snaží se balancovat mezi oběma možnostmi.
Braunova kuželová projekce v prostoru. Lze pohybovat modrým bodem na sféře.
Umístíme-li kulovou plochu tak, aby nárysna procházela jejím středem, můžeme pak do nárysny kuželovou plochu snadno rozvinout podle jejího průniku s nárysnou. Rozvinutá kuželová plocha bude mít vrcholový úhel roven 180° a bude navazovat na průmět kuželové plochy.
V prostoru se rovnoběžky zobrazí na rovnoběžkové kružnice kuželové plochy a poledníky na její spádové přímky. V rozvinutí tedy rovnoběžky budou reprezentovány soustřednými polokružnicemi a poledníky dvěma úsečkami navzájem pootočenými o 90°.
Bod daný souřadnicemi pak zobrazíme nejprve promítnutím rovnoběžky na kuželovou plochu a následným dorýsováním půlkružnice. Poledník pak zobrazíme jako dvojici úseček, kde jedna je od průmětu hlavního poledníku otočena o polovinu zeměpisné délky. Druhou část průmětu získáme otočením o 90°.
Na appletu níže vidíte konstrukci rovnoběžek a poledníků (po zaškrtnutí políčka). Modrými body lze hýbat. Dále se po zaškrtnutí políčka zobrazí otočená rovnoběžka a samotný poledník.
Braunova kuželová projekce v promítání. Pohybujte modrými body.
Braunova kuželová projekce zemského povrchu