Grafisches Ableiten und Ableitungsfunktion
Aus der Ableitung wird eine eigene Funktion
Fahren Sie im linken Diagramm mit dem Punkt P über den Graphen. Die Steigung an der entsprechenden x-Stelle wird automatisch im rechten Diagramm aufgetragen. Die x-Koordinate des Punktes M ist die entsprechende x-Stelle; die y-Koordinate ist die Steigung m.
Verbindet man alle Punkte M, so entsteht ein neuer Graph. Tippen Sie in das rechte Feld den Term dieses neuen Graphen ein.
Wiederholen Sie die Aufgabe mit einer anderen Funktion f, zum Beispiel mit f(x)=x³.
Die Ableitungsfunktion
Wird jeder x-Stelle die jeweilige Ableitung einer Funktion f zugeordnet, so spricht man von einer Ableitungsfunktion:
Aufgabe: Grafisches Ableiten per Hand
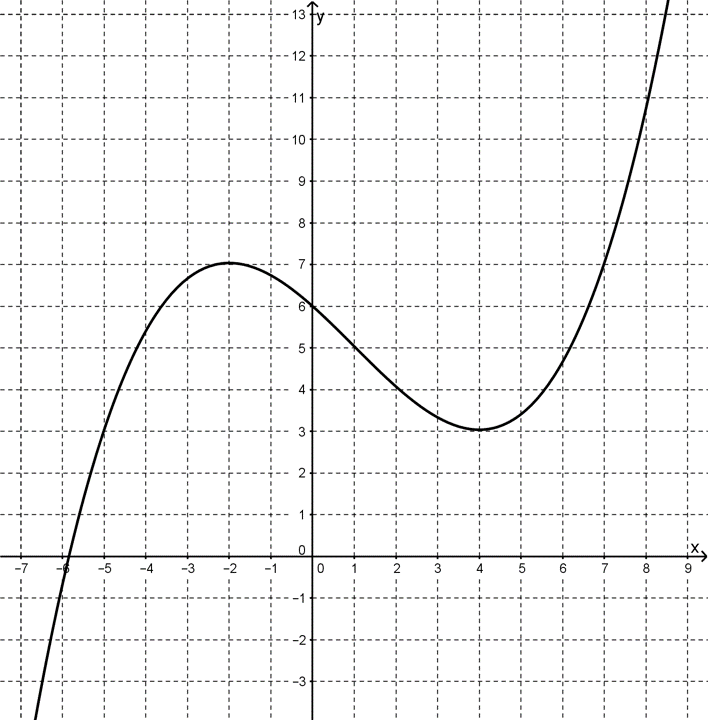
Drucken Sie dieses Diagramm aus und erstellen Sie Schritt für Schritt den Graphen der Ableitungsfunktion, indem Sie an jeder Stelle die Tangente einzeichnen und mittels Steigungsdreieck die Steigung ablesen. Tragen Sie die gemessenen Steigungen an der jeweiligen Stelle als Punkt in das Diagramm ein.
Vorlage fürs grafische Ableiten auf Papier
Grafisches Ableiten Musterlösung
Ableitungsfunktion überprüfen
Aufgabe
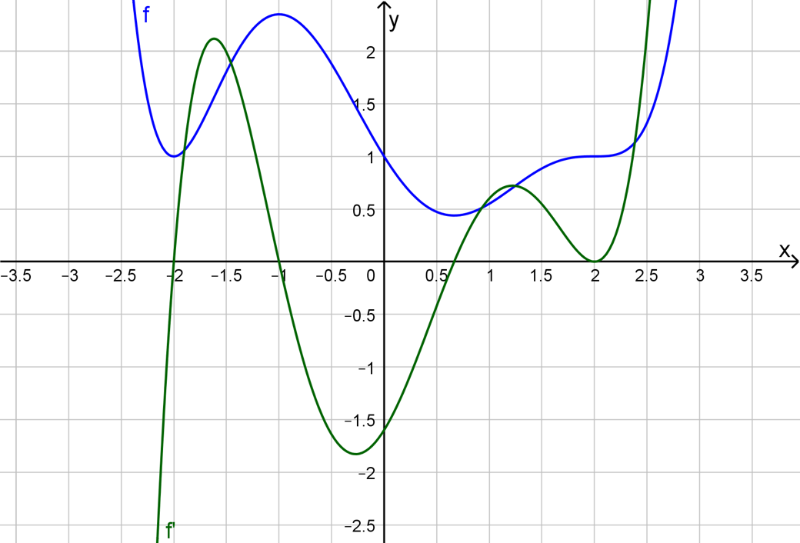
Überprüfen Sie im nächsten Diagramm, ob der grüne Graph tatsächlich zur Ableitungsfunktion f' der Funktion f passt, deren Graph in blau dargestellt ist.
Schreiben Sie zu mindestens fünf charakteristischen Stellen: "An der Stelle ??? passt f' zu f, weil ..."
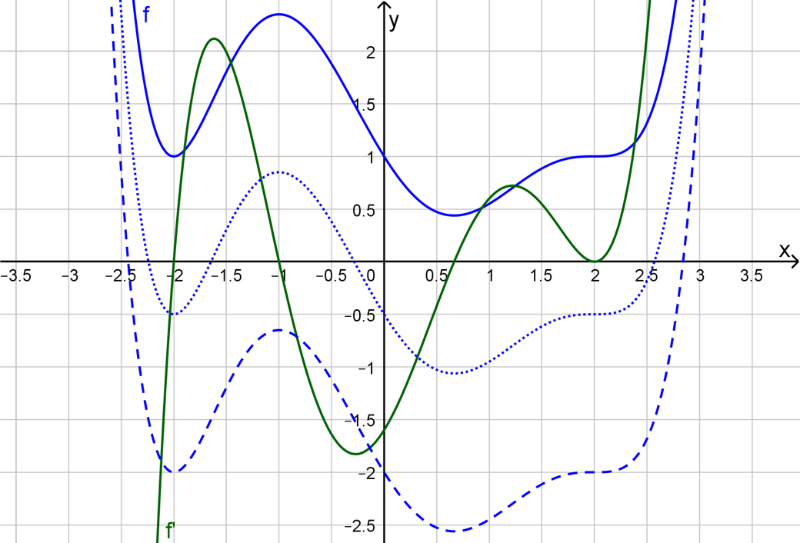
Verständnisfrage
Wie ändert sich der Graph der Ableitungsfunktion (grün), wenn statt dem durchgezogenen blauen Graphen der gepunktete bzw. der gestrichelte abgeleitet wird?