14.三角比の利用
1.実物への利用
このページは電子ブック「探求 数学Ⅰ」の一部です。
<測量と計算>
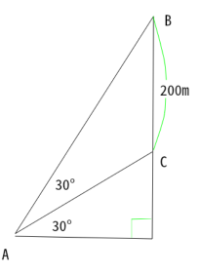
(例)交差点Aから等しい距離にある、高さの差が200mのタワーBとタワーCがある。
Aからみた頂上までの仰角はタワーBが60°で、タワーCが30°とすると、
タワーBの高さは何mか?
AからBとCまでの距離は等しいので、
高さの比は、tan60°:tan30°=。
だから、x=3x-600。x=300(m)
2.立体への利用
<多面体と球体>
底面が多角形の柱体は、側面が底面の辺の数だけある。
側面を1つにして展開すると2底面がある。
底面が多角形のすい体は、側面が底面の辺の数だけある。
側面を1つにして展開すると底面が1つある。
底面が多角形の柱体・すい体に他の立体を外接・内接する場合、
接点を通る断面図をかく。
断面図の平面図形における三角形や円のしくみに着目して、
相似や三角比などを利用する。
(例)「底面が1辺6の正方形KLMNで、のこりの辺も6の四角すいPKLMNがある。
この四角すいに外接する球体、内接する球体の半径」は?
底面の対辺の2つの中点をA,Cとし、ACの中点をHとする。
AC=KL=6。対角線KM=
・△PKMの外接円が中心Oを含む外接球体の断面。
PH=KH=で、角PKM=角PMK=45°だから、
Hが外接球体の中心Oになる。半径は
・△PACは二等辺三角形で、この内接円が中心Iを含む内接球体の断面。
AH=6/2=3、PA=PC=。PH=。S=
一方で、△PAC の周囲はから、
S=。
r=
3.三角形の特徴
<関係式の単純化>
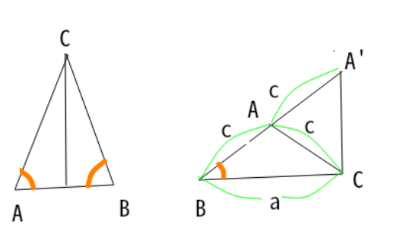
(例)△ABCでsinAcosB=sinBcosAが成り立つときの特徴は?
式変形すると、だから、tanA=tanB。だから、
角A=角Bの二等辺三角形になる。
(例)△ABCで2cosBsinC=sinAが成り立つときの特徴は?
正弦定理から、だから、
余弦の定義から、BAを延長して、cの2倍のc'となる頂点A’をとる。
△A'BCは直角三角形で、Aが外接円の中心、半径がcになり、
AB=ACの二等辺三角形になる。
4.内接四角形
<内接四角形への利用>
対角線の2乗を、余弦定理によって、4辺とコサインで2通りに表すことができる。
また、内接四角形の対角のコサインは異符号で同じ大きさになることも利用できる。
また、内接四角形の対角のサインが等しいことが面積計算に使えるね。
コサインからサインを求めると、面積の計算に利用できる。
三角形の面積は、1/2×2辺の積×間角のサインだからね。
(例)「AB,BC,CD,DAの順の四角形が円に内接している。ACとBDの交点がEならBE:ED」は?
sinB=sin(180-B)だから、三角形ABC:三角形ADC=1/2・8・3sinB: 1/2・5・5sin(180-B)=24:25
BE:EDはACを底辺とするときの三角形ABCと三角形ADCの高さと一致するから、
面積比とも一致する。だから、BE:ED=24:25。
(例)「AB,BC,CD,DAの順の四角形が円に内接している。sinBと内接四角形の面積」は?
cosB=x、AC=yとおく。cos(180°-B)=-xで、
余弦定理から、y2=52+42-2・5・4・x=12+42-2・1・4・(-x)。
41-40x=17+8xとなるから、24=48x。x=1/2=cosB。
B=60°となり、sinB==sin(180°-B)。
△ABC+△ADC=
(例)「AB,BC,CD,DAの順の四角形が円に内接している。ACの長さと内接四角形の面積」は?
cosB=x、AC=yとおく。cos(180°-B)=-xで、
余弦定理から、y2=62+52-2・6・5・x=32+52-2・3・5・(-x)。
61-60x=34+30xとなるから、27=90x。x=3/10=cosB。
y=√(61-60×3/10)=√43。
sinB=√(1-(3/10)2)=√91/10=sin(180-B)°
△ABC+△ADC=
<一般化してみよう>
「AB,BC,CD,DAの順にp,q,r,sの四角形が円に内接している。ACの長さと内接四角形の面積」は?
cosB=x、AC=yとおく。cos(180°-B)=-xで、
余弦定理から、y2=p2+q2-2・pq・x=r2+s2-2・rs・(-x)。
p2+q2-(r2+s2)=2・(pq+rs)x。x==cosB。
・AC=y=√(p2+q2-2・pq×((p2+q2-(r2+s2))/2(pq+rs))=
・sinB=sin(180-B)°=
・S=△ABC+△ADC=1/2(pq・sinB + rs・sin(180-B))=
(参考)
上の最後の式で内接四角形の4辺をp,q,r,sのかわりにa,b,c,dにする。
t=p+q+r+sのかわりにs=1/2(a+b+c+d)にする。
そうすると、分母の4を√の中にいれて、4・4=16=2・2・2・2にとなる。
だから、(t−2p)/2=(s-a)のように、4つのカッコがすべて変換できて分母の4が消える。
S=√(s-a)(s-b)(s-c)(s-d)(s=1/2(a+b+c+d)) となる。
これをブラマグプタの公式と呼ぶらしい。d=0として、内接四角形を三角形にしたとき
S=√(s-a)(s-b)(s-c)s (s=1/2(a+b+c))となる。
これはヘロンの公式と同じだね。