Sinus und Cosinus am Einheitskreis
Aufgabe:
Lies dir folgende Informationen durch und bearbeite den unten fett abgedruckten Arbeitsauftrag.
Informationen
Bisher haben wir Sinus, Cosinus und Tangens in rechtwinkligen Dreiecken angewendet. Dabei war der Winkel , auf den wir Sinus, Cosinus oder Tangens angewendet haben, immer zwischen 0° und 90° groß.
Nun möchten wir Sinus, Cosinus und Tangens auch für Winkel definieren, die größer als 90° sind. Dafür verwendet man den Einheitskreis.
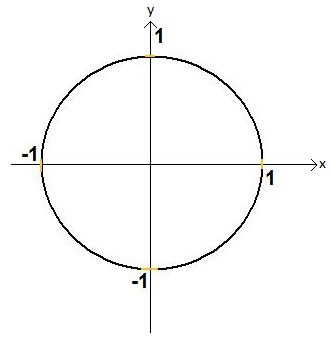
Lässt man nun einen Punkt auf dem Einheitskreis entlanglaufen, so entstehen rechtwinkelige Dreiecke (siehe dynamische Abbildung unten). Dabei liegt der rechte Winkel immer an der x-Achse und die Hypotenuse wird aus dem Radius des Einheitskreises gebildet. Die Länge der Hypotenuse ist also immer 1.
Bewegt man in der dynamischen Abbildung P auf dem Kreisviertel im ersten Quadranten, so ergibt sich immer ein rechtwinkliges Dreieck mit einem Innenwinkel . Da die Hypotenuse dem Radius des Einheitskreises entspricht und somit die Länge 1 besitzt, gilt immer:
von P (blaue Strecke)
von P (rote Strecke)
Bewegt man P aus dem ersten Quadranten heraus, so ist größer als 90° und kein Innenwinkel des Dreiecks mehr. Die obige Definition lässt man jedoch weiterhin gelten:
von P
von P
Auf diese Weise lassen sich Werte für und definieren, auch wenn größer ist als 90°. Diese Werte können nun - anders als vorher - auch negativ sein, wenn die x- oder y-Koordinate im negativen Bereich liegt.
Wir können nun also mithilfe des Einheitskreises Sinus und Cosinus für alle Werte zwischen 0° und 360° angeben.
- Vollziehe das nochmal an der folgenden Abbildung nach!
- Zeichne oder kopiere einen (ausreichend großen!) Einheitskreis in deine Doku und erkläre daran (in Stichpunkten) die Definition von Sinus und Kosinus!