Graph theory (AIHL 3.15, 3.16) - Part 5 Chinese Postman Problem
Inquiry questions
| Factual Questions: What is the Chinese Postman Problem (CPP) and how is it defined in the context of graph theory? How does the CPP differ from the Travelling Salesman Problem (TSP)? Describe the steps involved in solving the CPP using graph theory algorithms. | Conceptual Questions: Why is the CPP considered a practical problem in real-world applications such as mail delivery or street cleaning? How does the concept of Eulerian circuits and paths apply to the CPP, and why is it important for finding a solution? In what ways do the requirements for a graph to be Eulerian or semi-Eulerian impact the approach to solving the CPP? | Debatable Questions: Is the algorithm for finding an optimal CPP route always the best approach for solving real-world routing problems, considering the complexity of urban layouts? Given the similarities and differences between the CPP and TSP, can strategies from solving one be effectively applied to the other? How significant is the role of graph theory in addressing logistical challenges, such as the CPP, in modern urban planning and operations? |
The Chinese Postman Problem (CPP) might sound like a complex topic, but it's actually something you might encounter without even realizing it. Imagine you're a mail carrier, and your job is to deliver letters to every street in your neighborhood. The CPP is all about finding the quickest way to do this, making sure you cover every street without walking more than necessary and end up back where you started. This isn't just about delivering mail, though; it applies to things like snow plowing, street sweeping, or any task where every part of a network needs to be visited.What makes the CPP different from problems like the Traveling Salesman Problem, which you might have heard about, is its focus. While the Traveling Salesman Problem is all about visiting points or places efficiently, the CPP cares about the paths or connections between these places. It's a real-world challenge you can visualize in your own neighborhood or city, making it a relatable and practical part of your studies in DP mathematics. You'll use math to figure out the best route that saves time and effort, skills that are super useful in many everyday situations.
Imagine you're planning a route to walk through every path in a park and return to where you started. If the park's layout allows you to do this without retracing any steps, it's called an Eulerian graph, meaning every junction connects an even number of paths. However, most parks aren't laid out this way, and you'll likely encounter junctions connecting an odd number of paths, requiring you to double back on some paths to cover the entire park.

The challenge here is to figure out the minimum number of paths you need to walk twice to make this possible. This involves identifying the junctions (vertices) where paths meet unevenly and then determining the least amount of extra walking needed, which is solved by the minimum-weight perfect matching problem. This mathematical strategy helps you find the most efficient way to complete your route, showcasing how math can optimize solutions to real-world problems.
For the existence of Eulerian trails it is necessary that zero or two vertices have an odd degree. If there are exactly two vertices of odd degree, all Eulerian trails start at one of them and end at the other.
A graph is Eulerian if it contains an Eulerian circuit, which is a closed path that visits every edge of the graph exactly once. For a graph to have an Eulerian circuit, every vertex in the graph must have an even degree, which means that an even number of edges must meet at that vertex.
Decide whether these graphs are Eulerian or not.
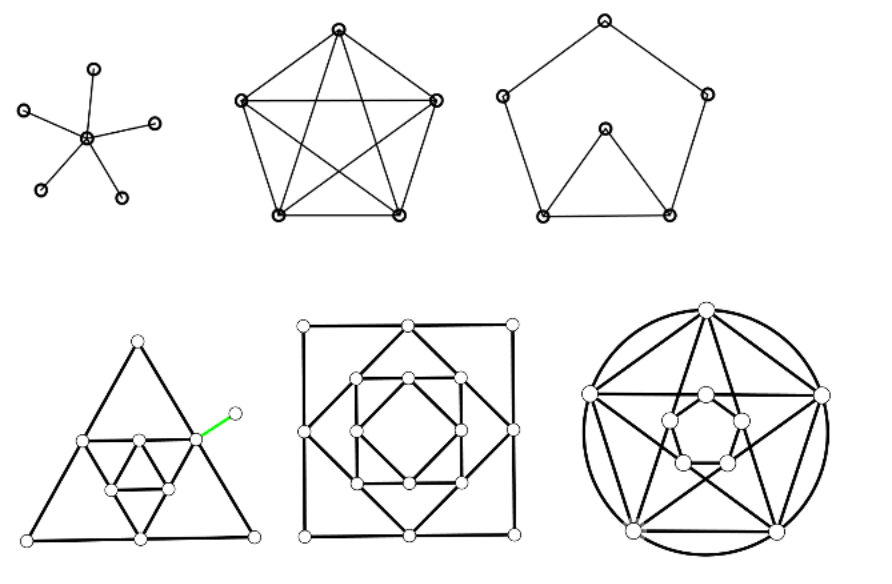
1 st graph is Eulerian
2nd graph is Eulerian
3rd graph is Eulerian
4th graph is Eulerian
5th graph is Eulerian
6th graph is Eulerian
An algorithm for finding an optimal Chinese postman route is:
Step 1 List all odd vertices.
Step 2 List all possible pairings of odd vertices.
Step 3 For each pairing find the edges that connect the vertices with the minimum weight.
Step 4 Find the pairings such that the sum of the weights is minimised.
Step 5 On the original graph add the edges that have been found in Step 4.
Step 6 The length of an optimal Chinese postman route is the sum of all the edges added to the total found in Step 4.
Step 7 A route corresponding to this minimum weight can then be easily found.
Chinese Postman Problem (See page 5-8 for worked example of the algorithm)
Reasoning for quiz answers
Graph 1 has a vertex with an odd degree (5), so it is not Eulerian.
Graph 2 has all vertices with even degrees (4), so it is Eulerian.
Graph 3 has vertices with both odd (3) and even (2) degrees, so it is not Eulerian. Although it has a pair of odd vertices and the rest are even so there exists an Eulerian trail so it is said to be Semi-Eulerian.
Graph 4 has vertices with odd degrees (3) as well as even degrees (4), so it is not Eulerian.
Graph 5 has all vertices with even degrees (4), so it is Eulerian.
Graph 6 has all vertices with even degrees (4 and 6), so it is Eulerian.

