5.

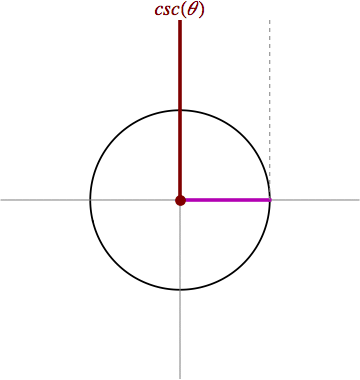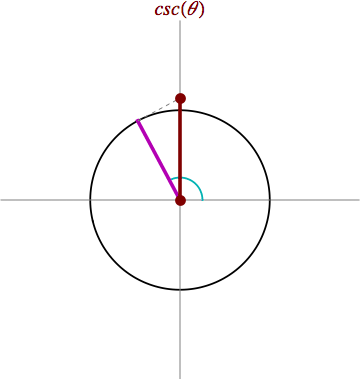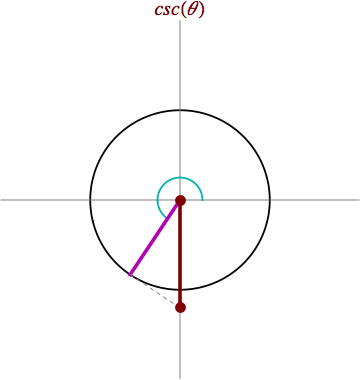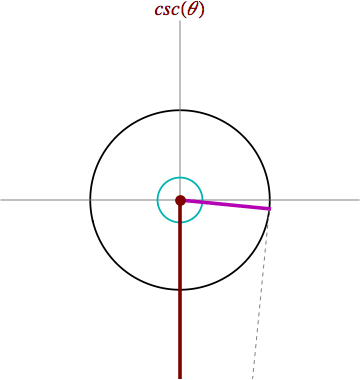
¿ Qué es la función cosecante ?
La función cosecante asocia a cada número real, x, el valor de la cosecante del ángulo cuya medida en radianes es x. La cosecante es la razón trigonométrica del seno. La cosecante del ángulo α de un triangulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto opuesto (a). Se expresa como

Tabla de valores de la función cosecante

Representación gráfica de la función cosecante en el intervalo [0;2π]
![Representación gráfica de la función cosecante en el intervalo [0;2π]](https://www.geogebra.org/resource/fzcememc/RYj8HfmtK2gHsN8S/material-fzcememc.png)
Características de la función trigonométrica cosecante
Dominio: - {n.} con n
Recorrido: ]1.-1[
No corta al eje X ni al eje Y
Intersecciones con el eje y: No posee
Es una función continua en los reales salvo en los punto en los que no
está definida.
La función es simétrica con respecto al origen
Presenta asíntotas en los puntos:
No es una función inyectiva.
No es una función sobreyectiva.
Máximos relativos:
Mínimos relativos:
La función cosecante es impar, ya que esto es, para todo elemento del dominio