Mediatriz y circuncentro
La mediatriz de un segmento AB es la recta perpendicular al segmento en su punto medio.
Propiedad: Los puntos de la mediatriz se encuentran a la misma distancia de A que de B.
Por tanto, la mediatriz divide al plano en dos regiones, los puntos que están más cercanos a A (la Zona A) y otra con los puntos que están más cercanos a B (la Zona B).
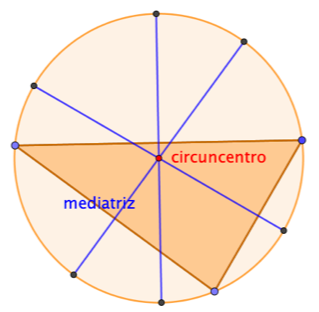
Si se construyen las mediatices de los tres lados de un triángulo se observa ¡que pasan por el mismo punto! Este punto se llama circuncentro (ver la Figura de arriba).
Por la propiedad anterior, el circuncentro está en las tres mediatices (la de los lados AB, AC y BC), por lo que está a la misma distancia de A, de B y de C. Esto hace que el circuncentro sea el centro de una circunferencia que pasa por A, B y C (la circunferencia circunscrita al triángulo ABC).
ACTIVIDAD: En la siguiente ventana realiza los siguientes pasos:
- Construye un triángulo ABC.
- Utiliza la herramienta de mediatriz
para construir las medianas de los 3 lados. - Renombra su punto de intersección como el circuncentro.
- Construye la circunferencia circunscrita.
Mueve la construcción moviendo alguno de los vértices A, B o C y observa qué ocurre con el circuncentro y la circunferencia circunscrita. Contesta a las siguientes preguntas:
¿El circuncentro se encuentra siempre en el interior del triángulo? ¿En qué casos no lo está?
¿El circuncentro siempre existe? es decir, ¿hay algún momento en donde no se pueda calcular? En ese caso, qué le ocurre a la circunferencia circunscrita?
Construye en la siguiente ventana un triángulo rectángulo, calcula su circuncentro y contesta a la pregunta que se hace a continuación.
En la construcción que acabas de hacer, ¿en dónde se encuentra exactamente el circuncentro? ¿Por qué?