Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Getting to Know Slope!

Author:Kristin Carbone, Jakob Swanson, Tim Brzezinski

SOME SIMPLE INSTRUCTIONS

1. Throughout the class, I would like you to work through this activity independently. *If you are stuck, ask your table partner! 2. If there are any questions that you would rather write or draw on a separate sheet of paper, that is fine. Mrs. Lyons and myself will look at them tomorrow.

Learning Objectives (Today we will...)

Comprehend the term “slope”. Draw a line on a coordinate grid given its slope and describe observations about lines with the same slope. Justify that we can use any two points on the line to calculate the slope.

Warm-up

1) Which is the best representation of a quotient?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

2. What do we call lines that do not intersect?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

3. How do you know?

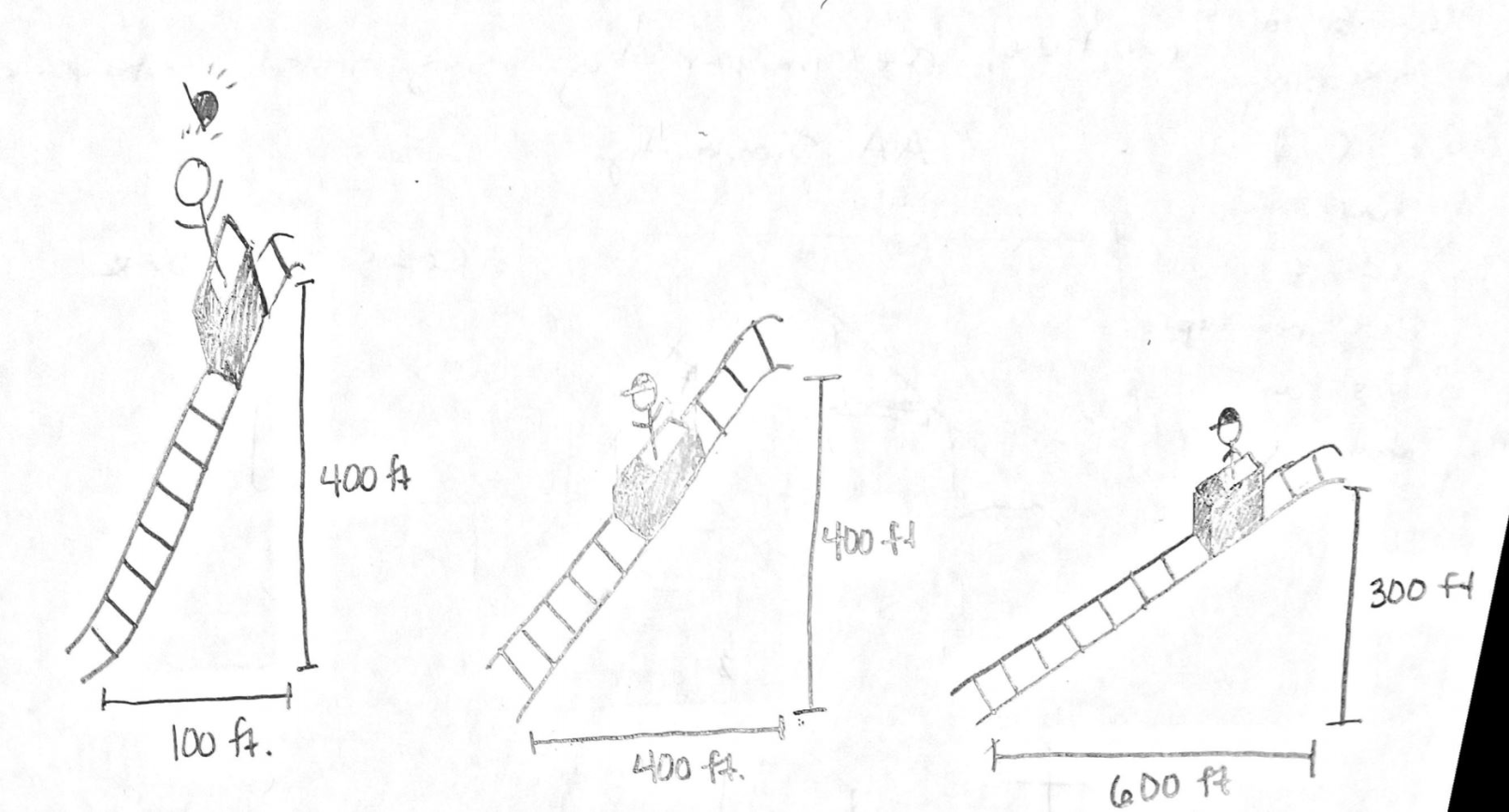
Out of the 3 rollercoasters that are drawn below which of them is the steepest? Describe your thinking.

Image

How do we determine slope?

Play around with the white dots on the line in the grid below. Notice how the ramp (slope) changes as you move the white dots below.

Question 1:

Notice what the slope equals in the upper left corner. Where on the triangle is the program getting this fraction from?

Question 2:

Create a triangle where the left white dot is BELOW the right dot. What is your slope? If a marble were on the ramp, would it be going up or down the ramp? Explain

Question 3:

Create a triangle where the left white dot is ABOVE the right dot. What happened to your slope? If a marble were on the ramp, would it be going up or down the ramp? Explain

Question 4:

Is the slope a quotient?

Select all that apply
  • A
  • B
Check my answer (3)

Explain your answer to number 4.

Lines with the same slope

In the activity below there are two lines. Using the bar in the top left, you can adjust the slope of the lines.

Question 1:

As you play around with the slope of the two lines, what happens when you set the slopes equal to each other? What do you notice?

Question 2:

Set one of the slopes to -2 and the other to 0.5. What kind of lines did you create? What do you notice about the lines?

Slope Triangles

In the ramp example above, there was a right triangle created to connect the two points. This triangle is called a slope triangle because it has a right angle and the hypotenuse (the longest side, across from the right angle) is along the line connecting two points. In the activity below, the orange triangle is also a slope triangle for the same reasons.
Check the boxes to the right of the graph to reveal the other triangles.

Is Triangle 1 a slope triangle?

Select all that apply
  • A
  • B
Check my answer (3)

Is Triangle 2 a slope triangle?

Select all that apply
  • A
  • B
Check my answer (3)

Why is Triangle 3 a slope triangle?

I claim that all 4 triangles in this activity can be used to find the slope of the line.

How would you defend this argument?

Extended Questions

Rewrite the following in your own words. (describe slope in your own words) The definition of “slope” is the quotient of the vertical distance and the horizontal distance between any two points on a line.

Your skateboarding down a hill, you're going pretty fast and you estimate the slope of the hill to be around -5. Your friend is skating right next to you and claims his hill has a slope is -6. Is this possible if you are on the same hill? Justify your answer.

Using what you know about slope, which rollercoaster from the drawings was actually the steepest? Justify your answer.

New Resources

Discover Resources

Discover Topics