À la recherche du coefficient (Partie II - Cas particulier)
Avant-propos
Nous savons donc maintenant que la relation de proportionnalité qui relie la longueur de l'arc et l'angle au centre fait aussi intervenir le rayon du cercle :
Nous allons cherche la valeur de ♥ et ainsi terminer notre recherche.Supprime le rayon du coefficient :
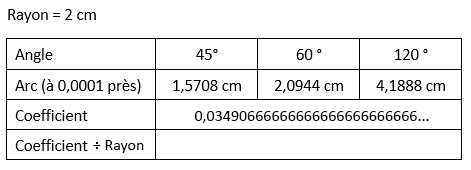
Analyse :
Le facteur ♥ obtenu est-il plus compréhensible ?
Une hypothèse (à vérifier plus tard)
Nous allons faire le pari que le nombre ♥ ne dépend plus d'autres facteurs et est une constante, quelque soit le cercle et l'angle choisis. Nous pourrons vérifier que c'est bien le cas plus tard. Et une rapide analyse de la construction de l'arc permettrait de s'en convaincre...
Si ♥ est un nombre qui ne change pas, alors pour déterminer sa valeur, il suffit de trouver un cas particulier* qui permet de relier l'angle et l'arc, pour un rayon donner.
(* Autre que le cas nul qui n'apporte aucune information dans une situation de proportionnalité.)
Un cas particulier : le tour complet !
L'arc intercepté par un angle au centre de 360° fait tout le tour du cercle : sa longueur est donc le périmètre du cercle. Or celui-ci vaut, par définition de π : 2π × rayon.
Ainsi, si nous choisissons un rayon de 1 cm, alors à un angle au centre de 360° est associé une longueur d'arc de 2π. Donc :
Et donc : ♥ = 2π/360°.Analyse :
♥ est-il bien un nombre qui ne dépend plus de rien ?
En reprenant le tableau ci-dessus, retrouve-tu bien le nombre mystère ♥ ?
Conclusion finale :
Quelle relation relie la longueur de l'arc de cercle à l'angle au centre ?