תכונות המעוין
המעוין כמקרה פרטי של מקבילית
לפניכם שרטוט דינמי של מקבילית.
נסו לערוך שינויים במקבילית כך שיתקבל בה זוג של צלעות סמוכות שוות.
שאלה:
מה קרה למקבילית כשעיצבנו אותה כך שיש לה זוג צלעות סמוכות שוות?
טענה:
מקבילית שלה זוג של צלעות סמוכות שוות היא מעוין.
הוכח זאת בעצמך...
נסו להוכיח את טענה זו בעצמכם במחברת.
כדי לעשות זאת ניזכר שוב בתכונות המקבילית:
* במקבילית הצלעות הנגדיות שוות ומקבילות זו לזו.
*במקבילית הזוויות הנגדיות שוות זו לזו.
*במקבילית סכום כל שתי זוויות סמוכות הוא 180 מעלות.
*במקבילית האלכסונים חוצים זה את זה.
כעת, נשרטט במחברת מקבילית ונסמן בה זוג צלעות סמוכות שוות. נסו להוכיח את הטענה במחברתכם
בהצלחה!
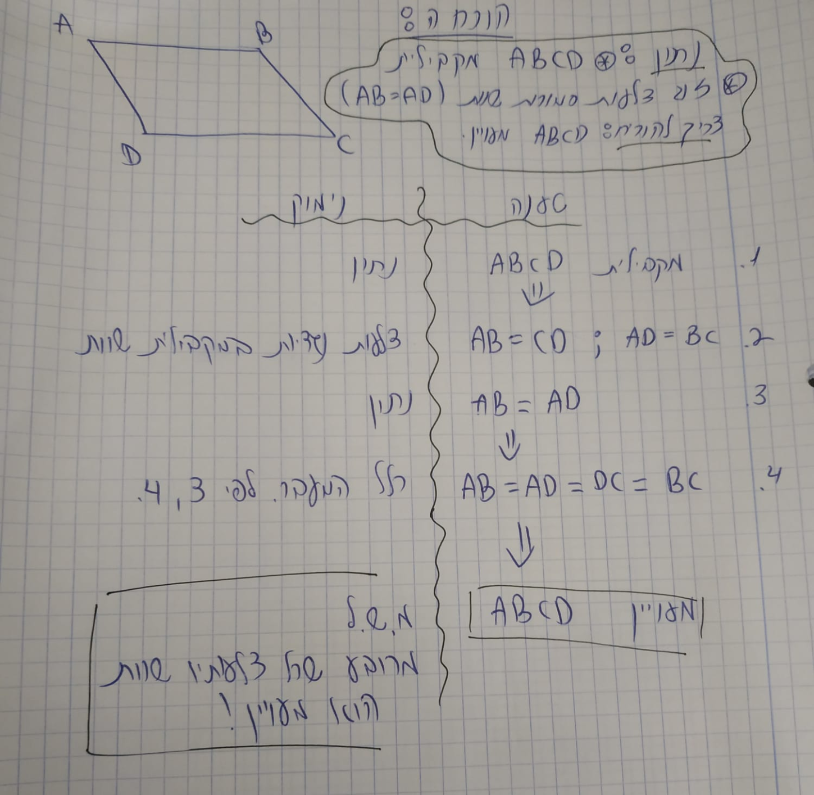
לפניכם ההוכחה:
ועכשיו, נתעמק בתכונות המעוין...
כפי שסיכמנו, המעוין הוא מקרה פרטי של מקבילית, ולכן כל מאפייני המקבילית חלים גם עליו.
לפניך שרטוט דינמי של מעוין. הסק את תכונות המעוין משרטוט זה.
שאלה:
מהן תכונות המעוין, כפי שהן מוצגות בשרטוט הדינמי?
ממה נובעות תכונות אלו?
התכונה "במעוין הצלעות הנגדיות מקבילות זו לזו" נובעת מתכונות המקבילית.
התכונה "במעוין הזוויות הנגדיות שוות זו לזו" גם היא נובעת מתכונות המקבילית.
התכונה "במעוין כל הצלעות שוות זו לזו" נובעת מהגדרת המעוין.
האלכסונים במעוין - תכונות נוספות
שאלה:
אם נעביר אלכסון אחד במעוין, מה ניתן לומר לגבי שני המשולשים שהתקבלו?
שאלה:
אם נעביר שני אלכסונים במעוין, כמה משולשים חופפים נקבל?
תזכורת:
משולש שווה שוקיים הוא משולש ששתיים מצלעותיו שוות זו לזו.
הצלעות השוות נקראות "שוקיים" והצלע השלישית נקראת "בסיס".
אחת התכונות במשולש שווה שוקיים היא: במשולש שווה-שוקיים, הגובה לבסיס, התיכון לבסיס, חוצה זווית הראש והאנך אמצעי לבסיס מתלכדים.
לפניכם ההוכחה למשפט:
משימה:
שרטטו במחברתכם מעוין על פי התכונות שלמדנו עד כה: כל הצלעות שוות, הצלעות הנגדיות מקבילות, הזוויות הנגדיות שוות. כמו כן, שרטטו את אלכסוני המעוין וזכרו את התזכורת לגבי משולשים שווי שוקיים. מה ניתן להסיק לגבי אלכסוני המעוין?
מסקנות:
במעוין,
אלכסוני המעוין מאונכים זה לזה.
אלכסוני המעוין חוצים זה את זה.
אלכסוני המעוין חוצים את זוויות המעוין.
תרגול תכונות המעוין:
בתרגילים הבאים מצאו את הגדלים החסרים.
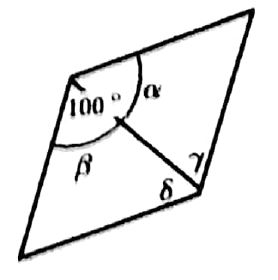
שאלה 1:
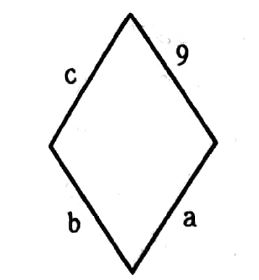
שאלה 2:
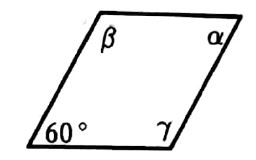
שאלה 3:
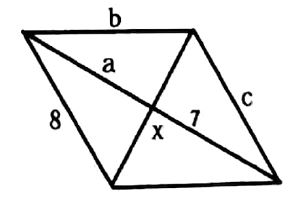
שאלה 4:
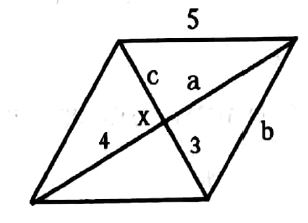
שאלה 5:
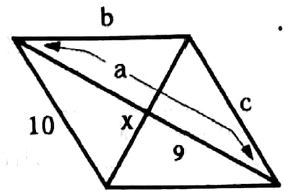
שאלה 6:
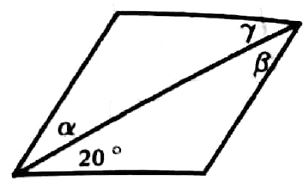
שאלה 7: