Graph theory (AIHL 3.15, 3.16) - Part 1 Definitions and basics
Inquiry questions
| Factual Questions: ]How are vertices and edges defined within the context of graph theory? What distinguishes a simple graph from a complete graph and a weighted graph? Explain the concepts of adjacent vertices, adjacent edges, and the degree of a vertex with examples. | Conceptual Questions: How do directed graphs differ from undirected graphs, and what implications do these differences have for graph traversal? Discuss the significance of the concepts of in-degree and out-degree in understanding directed graphs. In what ways do trees, as a type of subgraph, uniquely contribute to the study of graph theory? | Debatable Questions: Considering the constraints and definitions of Eulerian and Hamiltonian paths, which concept offers greater insight or utility in solving real-world problems? Can the distinction between simple, complete, and weighted graphs be seen as merely theoretical, or do these distinctions have practical implications in fields like computer science and network analysis? Is the classification of graphs into directed and undirected overly simplistic given the complexity of modern networked systems? |
Definitions
Graphs: A graph is a collection of points, called vertices, which may be interconnected by lines called edges.
Vertices: Also known as nodes, these are the fundamental units from which graphs are formed.
Edges: These are the connections between vertices in a graph.
Adjacent vertices: Two vertices are adjacent if they are connected by a single edge.
Adjacent edges: Two edges are adjacent if they share a common vertex.
Degree of a vertex: This refers to the number of edges incident to (or emanating from) a vertex.
For example,
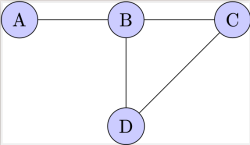
Adjacent vertices
Vertices A and B are adjacent because they are connected by a single edge.
Similarly, B and D are adjacent, as are C and D.
Adjacent edges
Edges A-B and B-C are adjacent because they share a common vertex, B.
Similarly, B-D and C-D are adjacent because they share vertex D.
Degree of a vertex
Degree of B is 3 because there are three edges incident to B (A-B, B-C, B-D).
Degree of C, and D are 2, as two edges are incident to each of these vertices.
Simple Graphs: A simple graph is an unweighted, undirected graph containing no loops (edges connected at both ends to the same vertex) and no more than one edge between any two different vertices..
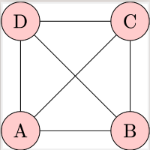
Complete Graphs: A complete graph is a simple graph in which every pair of distinct vertices is connected by a unique edge. This means in a complete graph with n vertices, every vertex has an edge to every other vertex
Weighted Graphs: A weighted graph is a graph in which each edge is assigned a weight or cost. This is useful in problems where the edges have some value, like the distance between two locations on a map.
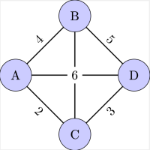
Connected: In the context of graph theory, a graph is connected if there is a path from any vertex to any other vertex in the graph. This means it's possible to get from any one vertex to any other by a sequence of edges. For example,
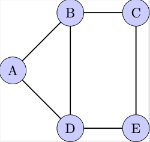
Directed Graphs: These are graphs where the edges have a direction, indicated by arrows. Each edge connects an ordered pair of vertices and points from one vertex (the tail) to another (the head). Directed graphs are also known as digraphs.
Strongly Connected: This term applies to directed graphs. A directed graph is strongly connected if there is a directed path from any vertex to every other vertex. That means you can start at any vertex and follow the direction of the arrows to reach any other vertex.
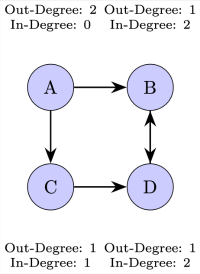
In-Degree and Out-Degree of a Directed Graph: The in-degree of a vertex is the number of edges pointing to it, while the out-degree is the number of edges that the vertex points to. In other words, in-degree counts the incoming arrows to a vertex, and out-degree counts the outgoing arrows from a vertex.
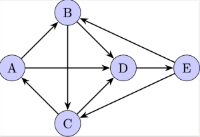
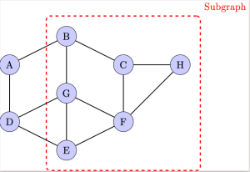
Subgraphs: A subgraph is a graph formed from a subset of the vertices and edges of another graph. It retains the connections that were present in the larger graph.
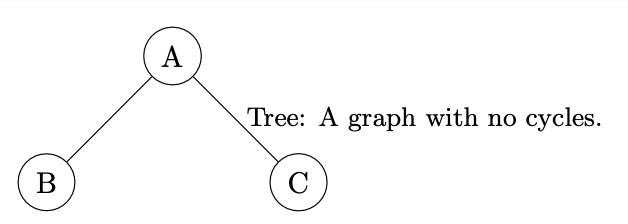
Trees: A tree is a special type of graph that is connected and has no cycles. This means there is exactly one path between any two vertices in a tree. Trees are a type of subgraph where any two vertices are connected by exactly one path.
AHL 3.16
Tree and Cycle Algorithms with Undirected Graphs: This refers to algorithms that operate on undirected graphs to identify trees (graphs with no cycles) and cycles (closed paths where the first and last vertices are the same).
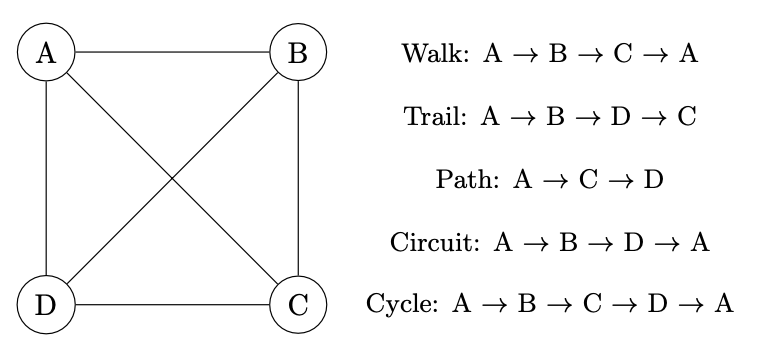
Walks, Trails, Paths, Circuits, Cycles: These are different ways to traverse graphs.
• Walk: A sequence of edges and vertices wherein vertices (and possibly edges) can be repeated.
• Trail: A walk where no edges are repeated.
• Path: A trail where no vertices are repeated.
• Circuit: A trail that starts and ends at the same vertex.
• Cycle: A circuit that only repeats the starting/ending vertex.
Eulerian Trails and Circuits: An Eulerian trail is a trail in a graph that visits every edge exactly once. If such a trail exists that starts and ends at the same vertex, it’s called an Eulerian circuit.
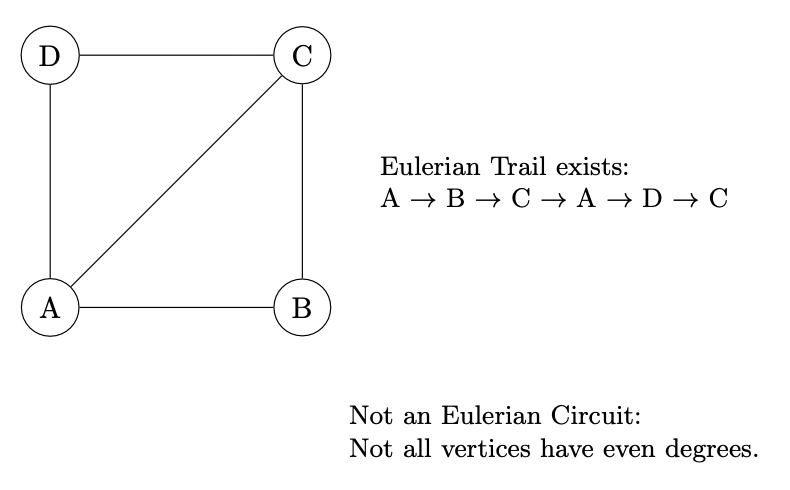
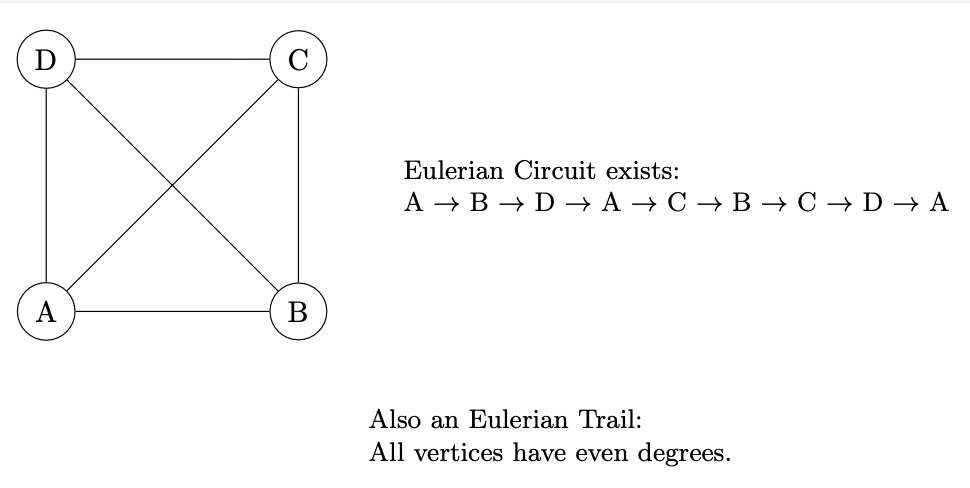
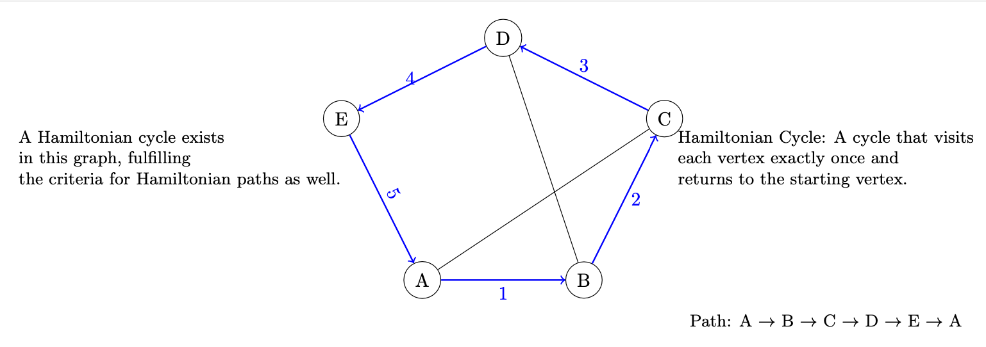
Hamiltonian Paths and Cycles: A Hamiltonian path is a path that visits each vertex in the graph exactly once; if the path is a cycle, then it’s called a Hamiltonian cycle.