Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Medidas de Posición: Cuartiles y Quintiles

Author:Felipe

Objetivo de Aprendizaje: MA08 OA 15

Mostrar que comprenden las medidas de posición, percentiles y cuartiles: - Identificando la población que está sobre o bajo el percentil - Representándolas con diagramas, incluyendo el diagrama de cajón, de manera manual y/o con software educativo. - Utilizándolas para comparar poblaciones.

Indicadores de Evaluación

- Organizan y agrupan datos en tablas o esquemas para formar distribuciones de frecuencias. - Calculan, describen e interpretan las medidas de posición (cuartiles y percentiles) - Representan las medidas de posición por medio de diagramas de cajón.
SECCIÓN I: CONECTANDO CON LA REALIDAD NACIONAL
Image
Lee la noticia del link y luego responde las preguntas. [b]https://www.latercera.com/noticia/estudio-gratuidad-para-20-mas-rico-cuesta-mas-del-doble-que-para-quintil-mas-vulnerable/[/b]
Lee la noticia del link y luego responde las preguntas. https://www.latercera.com/noticia/estudio-gratuidad-para-20-mas-rico-cuesta-mas-del-doble-que-para-quintil-mas-vulnerable/

Pregunta 1. Desde la noticia, ¿qué idea puedes extraer de lo que significan los quintiles socioeconómicos?

Pregunta 2. Al referirnos a quintiles, ¿en cuántos grupos se divide a la población?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Definición de quintiles

Los quintiles son cuatro valores que dividen los datos ordenados de menor a mayor en cinco parte iguales. Los quintiles son datos bajo los cuales se acumula aproximadamente el 20%, 40%, 60% y el 80% de los datos estudiados.
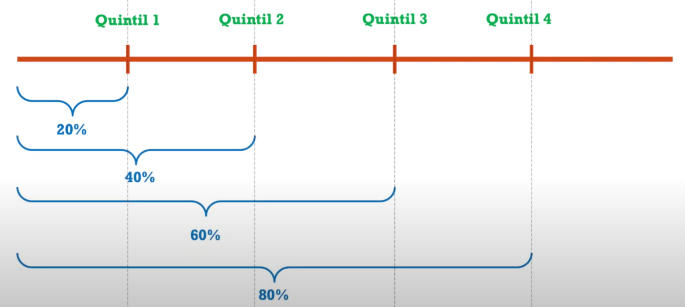
Image
Entonces, considerando este párrafo de la noticia, responde las preguntas 3 y 4.
Image

Pregunta 3. Desde la definición de quintiles, ¿es correcta la denominación de "quinto quintil"? ¿Por qué?

Check my answer

Pregunta 4. ¿A qué se quiso referir la periodista con la denominación de "quinto quintil"?

Select all that apply
  • A
  • B
Check my answer (3)
SECCIÓN II: CALCULANDO QUINTILES

¿Cómo se calculan los quintiles?

Revisa el ejemplo del siguiente video:

Pregunta 5. El ejemplo consideraba un conjunto de 14 datos, y a partir de esa cantidad es posible obtener exactamente 5 grupos con igual cantidad de datos en cada uno. ¿Qué cantidad de datos hay que tener para que cada grupo que se forme tenga 3 elementos cada uno?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Pregunta 6. ¿En qué posiciones se hallarían los 4 quintiles para un conjunto de 20 datos?

Revisa el siguiente video que muestra el algoritmo para determinar la posición de quintiles en cualquier conjunto de datos

Pongamos en práctica lo aprendido hasta ahora

Pregunta 7. Dado el siguiente conjunto de datos: 2 - 5 - 9 - 3 - 13 - 10 - 10 - 6 - 7 ¿Cuál es el valor del segundo quintil?

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)

Pregunta 8. Sabiendo que los quintiles son los 4 valores que dividen a un conjunto de datos en 5 grupos, si ahora quisiéramos dividir al conjunto de datos en 4 grupos, ¿cómo crees que se llamaría esa medida de posición?, ¿cuántos son?

Check my answer

Pregunta 9. ¿Cuál sería la fórmula para hallar la posición (P) de las medidas al dividir el conjunto de datos en 4 grupos? (con i=1,2,3 y N=cantidad de datos)

Select all that apply
  • A
  • B
  • C
  • D
Check my answer (3)
SECCIÓN III: ¡A PRACTICAR!

Práctica 1

A continuación hay un diagrama de puntos que muestra la duración de los viajes en autobús de Elena a la escuela, durante 12 días.
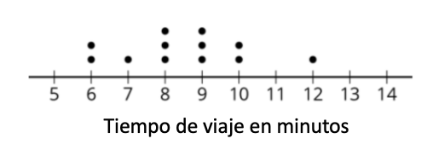
Image

Pregunta 10. ¿Cuál es el mínimo y máximo de los datos?

Check my answer

Pregunta 11. Calcula el cuartil 1 (Q1), cuartil 2 (Q2) y cuartil 3 (Q3)

Check my answer

Rango Intercuartil

Una forma de describir la dispersión de valores en un conjunto de datos es el rango intercuartil (RIQ), que corresponde a la diferencia entre el Q3 y el Q1.

Pregunta 12. ¿Cuál es el rango intercuartil (RIQ) de los tiempos de viaje de Elena?

Check my answer

Pregunta 13. ¿Qué fracción (o porcentaje) de los datos se encuentran entre los cuartiles inferior (Q1) y superior (Q2)?

Check my answer

Práctica 2

Acá te presentamos dos diagramas de puntos más
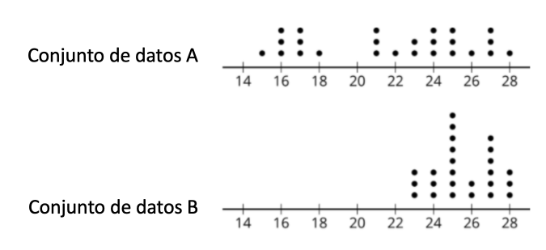
Image

Pregunta 14. ¿Qué conjunto de datos tiene el RIQ más pequeño?

Select all that apply
  • A
  • B
Check my answer (3)

Diagrama de cajón

Un diagrama de cajón es una representación visual que muestra una distribución de datos, basada en un resumen de cinco números: el mínimo, el primer cuartil, la mediana (segundo cuartil), el tercer cuartil y el máximo.
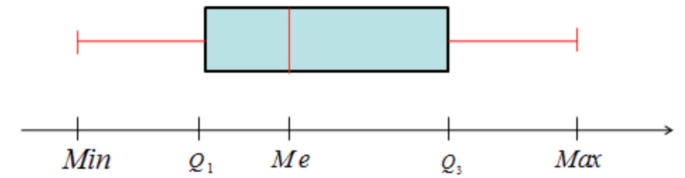
Image

Práctica 3

El siguiente applet muestra un diagrama de cajón para un conjunto de 17 calificaciones en una prueba.

Pregunta 15. El deslizador "Nota" corresponde a la nota nº17 de la vista de hoja de cálculo. Ubica el deslizador en 80 y luego muévelo hasta 100. ¿Por qué el promedio varía conforme cambia la nota nº17 mientras que las medidas de posición no se alteran?

Pregunta 16. Respecto a la pregunta anterior, ¿por qué varían algunas medidas de posición al mover el deslizador a valores menores a 80?

New Resources

Discover Resources

Discover Topics