Polinomios: Una interesante aplicación
El Cometa Hartley-2

Un Planteamiento: modelación del Cometa Hartley-2 mediante una función polinómica
Supóngase que el perfil del núcleo del cometa se puede aproximar por la siguiente función:
A medida que avancemos en nuestro estudio, podremos obtener información interesante mediante el uso de herramientas matemáticas.
Veamos cómo es la gráfica de dicha función, y de allí, cómo es el perfil del cometa...
Gráfica de la función que modela al perfil del cometa
¿Cómo entender el applet de arriba?
Fíjense chicos y chicas...
La curva verde es la gráfica de la curva que modela al perfil, es decir, la línea que bordea al cometa...
Mientras que, la línea roja que se sobrepone a la verde, es el perfil, la silueta del cometa de nuestro ejemplo.
¿Tiene sentido?
Observa como en la columna de la izquierda, si haces click en los redondos de colores, aparecen y desaparecen la curva y la silueta, dependiendo de qué quieres ver...
Cálculo del volumen del cometa
Una aplicación del modelo que tenemos, que aproxima la silueta del cometa es la posibilidad de aproximar su volumen...
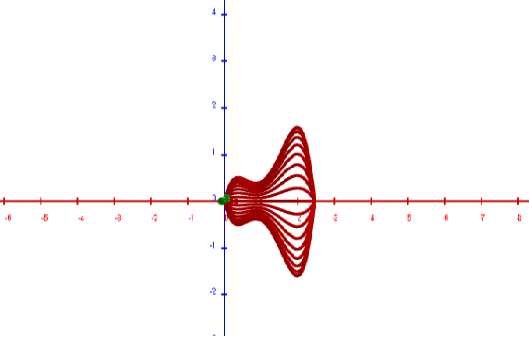
Veamos el siguiente dibujo, lo realicé en el graficador de 3 dimensiones de Geogebra (ya les enseñaré a usarlo), rotando la silueta alrededor del eje x
Imagen creada al rotar la silueta modelada por nuestro polinomio
Dejo una pregunta... quizá la respuesta la tengamos de futuros contenidos...
¿A alguien se le ocurre cómo podríamos calcular el volúmen de esta figura?