Franson – Bernex – Gisin
Mit freundlicher Genehmigung von Michael Rode.
In dem Doppel-Interferometer nach Franson werden von einer Quelle aus Photonenpaare in zwei Michelson-Interferometer eingespeist. Die Eigenschaften der Quelle bewirken, dass die Wellenlänge der beiden Photonen eines Paars in einem Bereich von etwa 2% um einen gemeinsamen Mittelwert schwanken. Die Photonen sind dabei wegen der Energie- und Impulserhaltung miteinander verschränkt, so dass die beiden zugehörigen Wellenlängen miteinander korrelliert sind.
Im Folgenden werden drei Experimente damit modelliert.
1. Kohärenzlänge (ein Interferometer allein)
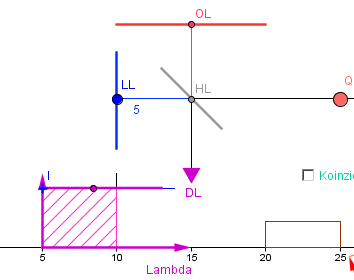
Hier wird nur mit dem linken Interferometer gearbeitet.
- Man stellt zunächst gleich lange Arme ein. Dazu dient der Schieberegler LageLinks, der in Einheiten von 5cm (obere Armlänge) kalibriert ist. Variation der Wellenlänge (durch beliebiges Hin-und Herbewegen des Schiebereglers LambdaL zeigt das erwartete Ergebnis: die Zählrate am Detektor DL bleibt unabhängig von der Wellenlänge konstant. Das zeigt der violett dargestellte Graph unter dem Detektor DL. Da die gemessene Rate einen Mittelwert über die Raten für alle Wellenlängen darstellt, wird die Fläche unter dem Graphen (durch Verschieben des Punktes I) bestimmt. Sie ergibt sich zu 1 (rechts neben den Bildern normiert als „pli“ angegeben). Nachweis des Photons in DL ist also ein sicheres Ereignis.
- Nun kann man den linken Arm des Interferometers verlängern. Dann beginnt die Zählrate abhängig von der Wellenlänge zu schwanken. Die Kohärenzlänge ist überschritten, wenn wegen der Variation der Wellenlänge alle Zählraten zwischen 0 und 1 auftreten, der Detektor DL also statistisch anspricht:
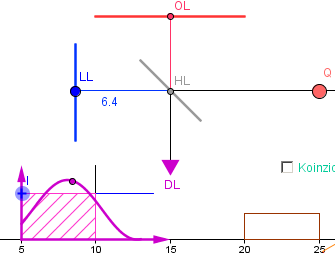
Im dargestellten Fall ist die gemittelte Zählrate schon deutlich unter 1. Zur Abschätzung des Integrals (Mittelwerts) wird der Punkt I nach Augenmaß so eingestellt, dass die Flächenstücke zwischen Mittellinie und Ratengraph gleich groß scheinen.
Der Wert wird schließlich 0,5 – wenn nämlich der Graph so aussieht:
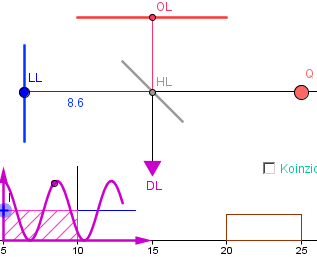
Jetzt ist die gemittelte Wahrscheinlichkeit für jeden der beiden Ausgänge des Interferometers gleich groß.
2. Koinzidenz (zwei Interferometer)
Man startet mit einer Einstellung gleicher Armlängen im linken Interferometer und deutlich verschiedener Armlängen im rechten (hier sind nur 5 bzw. 10 cm möglich).
Mit dem Kontrollkästchen „KoinzidenzEin“ kann man die Koinzidenzrate darstellen lassen. Das Ergebnis ist der mittlere der drei gezeigten Graphen.
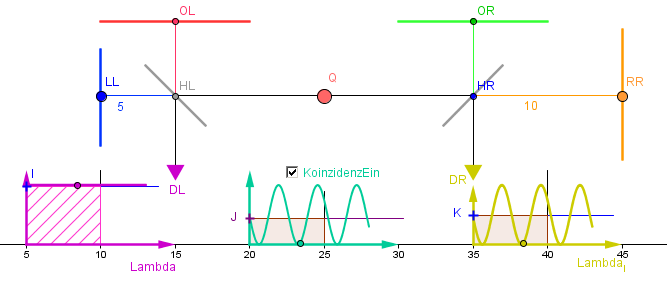
Bei den vorliegenden Einstellungen liegt die Vermutung nahe, dass die gemittelte Koinzidenzrate sich als das Produkt der beiden Einzelraten auffassen lässt. Das kann man allerdings sogleich widerlegen, wenn man auch das linke Interferometer „verstimmt“, bis zum Extremfall, in dem die beiden horizontalen Arme in den beiden Interferometern gleich lang sind.
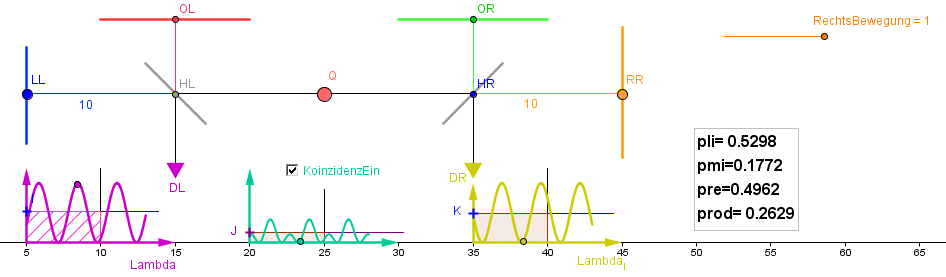
In der abgebildeten Situation ist die mittlere Koinzidenzrate pmi deutlich kleiner als das Produkt prod der beiden gemittelten Raten pli bzw. pre!
Klassisch würde man versuchen, den Vorgang durch einen zweistufigen Baum zu beschreiben:
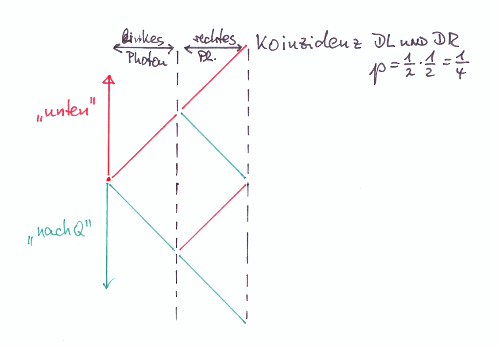
Anwendung der Pfadregeln sagt eine Koinzidenzwahrscheinlichkeit von ¼ voraus. Die Voraussetzung einer Nachweiswahrscheinlichkeit von 0,5 für jeden der beiden Detektoren zeigt die Modellation auch (trotz Augenmaß hinreichend) genau.
Die gemittelte Koinzidenzrate allerdings ist erkennbar verschieden davon!
Dieses Verhalten ist klassisch nicht zu erklären.
Nach den Regeln zur angemessenen Beschreibung eines superponierten Systems muss man die Übergangswahrscheinlichkeiten aus diesem Baum in ein Produkt von Zeigern übersetzen:
Koinzidenz tritt auf, wenn
(PhotonLinks_refl_DL und PhotonRechts_refl_DL) oder (PhotonLinks_trans_DL und PhotonRechts_trans_DR) oder (PhotonLinks_trans_DL und Photon_rechts_refl_DR) oder (PhotonLinks_refl_DL und PhotonRechts_trans_DR)
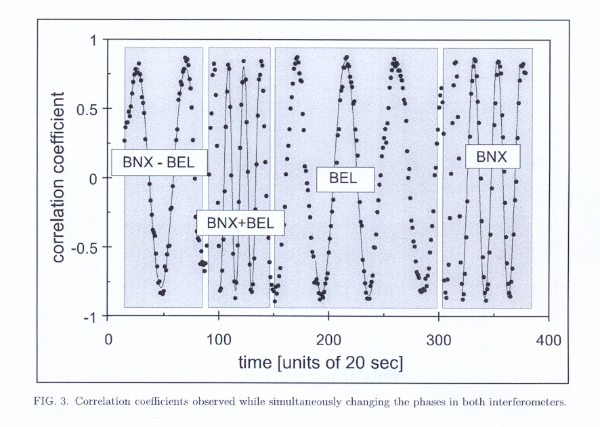
Die und-Relation bedeutet ein Produkt aus zwei Zeigern, die oder-Relationen bedeuten Summen von Termen - sie stehen für die Superposition. Die Umsetzung dieser Beschreibung führt in der Modellation auf die in der Mitte farbig dargestellten vier Zeiger und auf die dargestellte Koinzidenzrate, die das Quadrat der Zeigersumme ist. Zur Bestimmung der jeweiligen gemessenen Rate muss man wieder nach Augenmaß die Fläche unter dem zugehörigen Graphen bestimmen. Es ist erstaunlich, dass zwei Interferometer trotz gleich großer Verletzung der Kohärenzbedingung und daher statistisch verteilter Zählrate konstante Koinzidenzraten liefern. Im Bernex-Experiment wurde der Abstand beider Endspiegel einzeln oder gleichzeitig auf einer Skala von wenigen Wellenlängen verändert. Das kann nachgebildet werden mit Hilfe des Schiebereglers DABSTAND oben in der Mitte. Ob und wie er auf die beiden Spiegel wirkt, wird mit den Reglern LinksBewegung bzw. RechtsBewegung eingestellt. Der Wert -1 erlaubt die Bewegung des betreffenden Spiegel in Schritten von DABSTAND nach links, +1 nach rechts. Null bedeutet: keine Bewegung dieses Spiegels. Eine quantitative Durchführung mit fest stehendem linken und bewegtem rechten Spiegel führt zu gemittelten Koinzidenzraten, die im folgenden Diagramm über der Variablen DABSTAND dargestellt sind: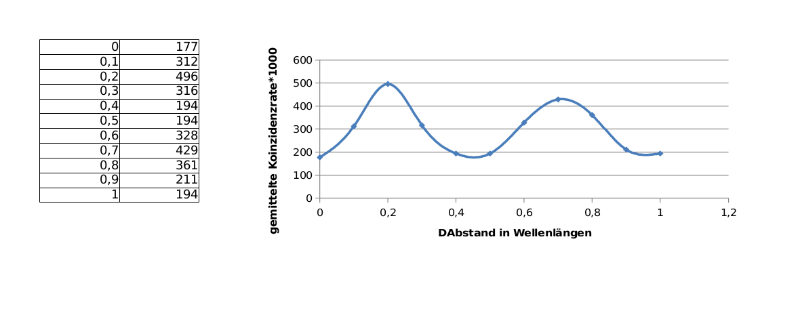
Das Ergebnis steht in guter Übereinstimmung mit den Ergebnissen des Bernex-Experimentes (W. Tittel, J. Brendel, N. Gisin, H. Zbinden: Long-distance Bell-type tests using energy-time entangled photons. arXiv:quant-ph/9809025v1 01Sep1998, S. 18; Bildausschnitt Bel)