POLIGONI ISCRITTI E CIRCOSCRITTI
ATTIVITA' 1: OSSERVA E DEDUCI
PRIMA SENZA MUOVERE LO SLIDER!!!
Osserva i punti di contatto tra la circonferenza e il triangolo.
Poi muovendo lo slider cosa puoi notare?
Rispondi di seguito al disegno.
POSIZIONI DELLA CIRCONFERENZA E DEL POLIGONO
RISPONDI ALLA DOMANDE
PRIMA DI MUOVERE LO SLIDER 1) I punti di contatto nella figura A, quanti sono e dove si trovano? A cosa corrispondono? 2) Nella figura A la circonferenza è esterna o interna? 3) I punti di contatto nella figura B dove si trovano e quanti sono? 4) Nella figura A la circonferenza è esterna o interna? DOPO AVER SPOSTANTO LO SLIDER 5) Cosa cambia?
DEFINIZIONE
Un poligono si dice inscritto in una circonferenza quando tutti i suoi vertici sono punti che appartengono alla circonferenza data. In questo caso la circonferenza si dice circoscritta al poligono.
Un poligono si dice circoscritto a una circonferenza quando tutti i suoi lati sono tangenti alla circonferenza data. In questo caso la circonferenza si dice inscritta nel poligono.
ATTIVITA' 2: E SE I POLIGONO NON SONO REGOLARI?
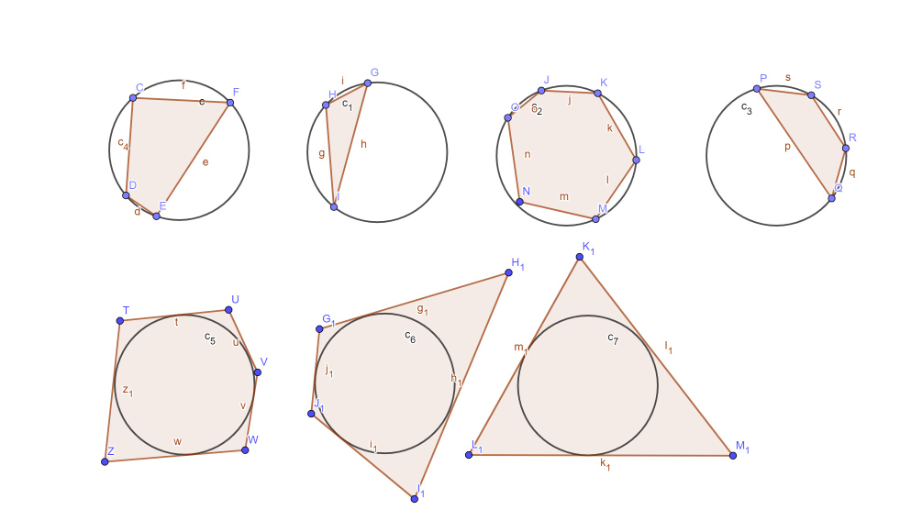
CIRCOSCRITTO E INSCRITTO
I poligoni della serie in alto sono ..
CIRCOSCRITTO E INSCRITTO
I poligoni della serie in basso sono ..
ATTIVITA' 3: CONDIZIONE DI INSCRIVIBILITA' E CIRCOSCRIVIBILITA'
DISEGNO 1)
-Traccia un triangolo qualsiasi utilizzando o
o  -Disegna le tre bisettrici degli angoli con
-Disegna le tre bisettrici degli angoli con . Il punto d'incontro si chiama INCENTRO e sarà il centro della circonferenza interna.
-Traccia la circonferenza con centro nell'incentro e utilizzando i tre vertici del triangolo.
DISEGNO 2)
- Traccia un triangolo qualsiasi utilizzando
. Il punto d'incontro si chiama INCENTRO e sarà il centro della circonferenza interna.
-Traccia la circonferenza con centro nell'incentro e utilizzando i tre vertici del triangolo.
DISEGNO 2)
- Traccia un triangolo qualsiasi utilizzando  o
o  .
-Disegna i tre assi dei lati i con
.
-Disegna i tre assi dei lati i con  . Il punto d'incontro si chiama CIRCOCENTRO e sarà il centro della circonferenza esterna.
- Traccia la circonferenza con centro nel circocentro e tangente ai tre la ti del triangolo.
. Il punto d'incontro si chiama CIRCOCENTRO e sarà il centro della circonferenza esterna.
- Traccia la circonferenza con centro nel circocentro e tangente ai tre la ti del triangolo.
 o
o  -Disegna le tre bisettrici degli angoli con
-Disegna le tre bisettrici degli angoli con . Il punto d'incontro si chiama INCENTRO e sarà il centro della circonferenza interna.
-Traccia la circonferenza con centro nell'incentro e utilizzando i tre vertici del triangolo.
DISEGNO 2)
- Traccia un triangolo qualsiasi utilizzando
. Il punto d'incontro si chiama INCENTRO e sarà il centro della circonferenza interna.
-Traccia la circonferenza con centro nell'incentro e utilizzando i tre vertici del triangolo.
DISEGNO 2)
- Traccia un triangolo qualsiasi utilizzando  o
o  .
-Disegna i tre assi dei lati i con
.
-Disegna i tre assi dei lati i con  . Il punto d'incontro si chiama CIRCOCENTRO e sarà il centro della circonferenza esterna.
- Traccia la circonferenza con centro nel circocentro e tangente ai tre la ti del triangolo.
. Il punto d'incontro si chiama CIRCOCENTRO e sarà il centro della circonferenza esterna.
- Traccia la circonferenza con centro nel circocentro e tangente ai tre la ti del triangolo.VERIFICA CHE I TRIANGOLI SIANO INSCRITTI E CIRCOSCRITTI.
ATTIVITA 4: TUTTI I POLIGONI SI POSSONO INSCRIVERE E CIRCOSCRIVERE?
1) Abbiamo osservato che tutti i poligoni regolari si possono inscrivere e circoscrivere.
2) Ti anticipo che anche tutti i triangoli si possono inscrivere e circoscrivere perchè è sempre possibile individuare l'incentro e il circocentro.
MA COSA SUCCEDE CON I QUADRILATERI?
PROVA TU STESSO:
DISEGNO 1) Traccia un rombo e individua l'incentro ed il circocentro. Se puoi costruisci la circonferenza circoscritta e inscritta
DISEGNO 2) Traccia un rettangolo e individua l'incentro ed il circocentro. Se puoi costruisci la circonferenza circoscritta e inscritta.
DISEGNO 3) Traccia un trapezio isoscele e individua l'incentro ed il circocentro. Se puoi costruisci la circonferenza circoscritta e inscritta.
COSTRUISCI I QUADRILATERI E CERCA DI SCOPRIRE SE SI POSSONO INSCRIVERE E/o CIRCOSCRIVERE
COSA HAI SCOPERTO?
Il Rombo si può inscrivere? Si può circoscrivere? Il Rettangolo si può inscrivere? Si può circoscrivere? Il trapezio isocoscele si può inscrivere? Si può circoscrivere?