2. Elementare Funktionen: Lineare Funktion - Infoblatt
Erstelle für ein altes Arbeitsblatt folgende Grafik als GeoGebra Datei!
Eine alte Grafik auf einem Infoblatt soll durch eine neue ersetzt werden. Erstellen Sie eine GeoGebra Datei, und fügen Sie ihre Grafik statt der untenstehenden Grafik ein.
Gehen Sie hierbei wie folgt vor.
Kopieren Sie diese Aktivität.
Erstellen Sie offline mit GeoGebra 5.0 eine Version, die ihren Ansprüchen genügt und laden Sie anschließend diese Datei hoch und ersetzen Sie die SW- Graphik durch ihre GeoGebra Datei.
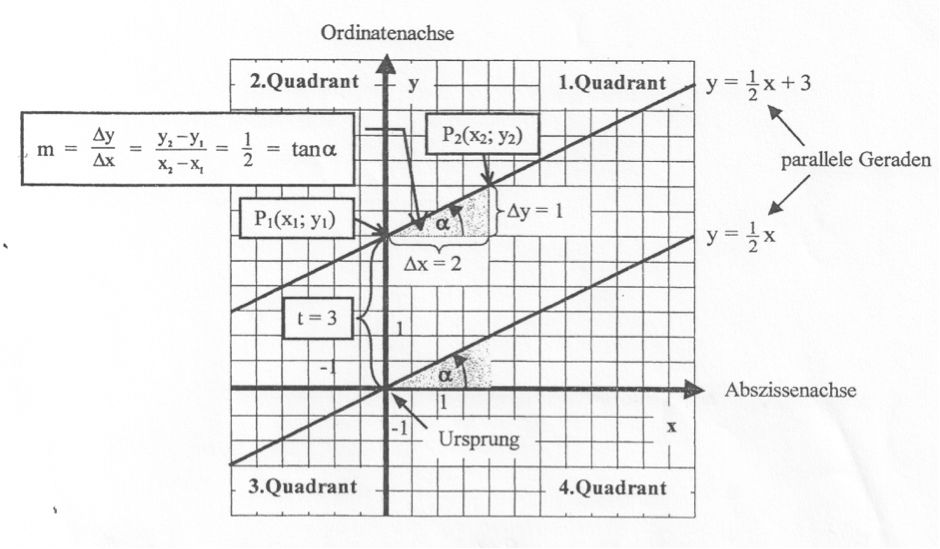
Da die Variable x in der Gleichung -0,5x + y = 3 nur in der ersten Potenz (x1) vorkommt, bezeichnet man sie als lineare Gleichung. Durch Auflösen dieser linearen Gleichung nach der Variablen y, erhält man die Normalform f: y = 0,5x
+ 3 der linearen Funktion. Da bei Funktionen der Wert der Variablen y immer vom Wert der Variablen x abhängt, bezeichnet man x als unabhängige Variable oder Argument und y entsprechend als abhängige Variable.
Die Menge der x-Werte, die durch die Funktion f abgebildet werden, bezeichnet man als Definitionsmenge ID der Funktion. Entsprechend bilden die y-Werte (Funktionswerte), die sich durch einsetzen von x in den Funktionsterm f
ergeben, die Wertemenge W der Funktion.
Die lineare Funktion f: y = 0,5x +3 lässt sich im Koordinatensystem graphisch als Gerade mit dem positivem Steigungsfaktor m = 0,5 und dem y-Achsenabschnitt t = 3 darstellen.
Der Steigungsfaktor m lässt sich mit Hilfe des eingezeichneten Steigungsdreiecks ablesen.
Auf der Geraden f: y = 0,5x +3 liegen alle Punkte P(x;y), die den Funktionsterm f erfüllen. Durch Parallelverschiebung dieser Geraden in den Koordinatenursprung
(Koordinatensystem – Mittelpunkt) ergibt sich die sogenannte Ursprungsgerade g: y = 0,5x