Näherungsweise Berechnung von Pi (Archimedes)
Ausgehend von einem Sechseck kann durch fortgesetzte Verdopplung der Seitenanzahl des Vielecks der Umkreis eines Kreises immer besser angenähert werden.
Archimedes berechnete auf diese Weise einen Näherungswert für Pi, indem er den Kreis durch ein 96-Eck annäherte.
Mit Hilfe der Tabellenkalkulation kann heutzutage ein Näherungswert für Pi einfacher und schneller ermittelt werden.
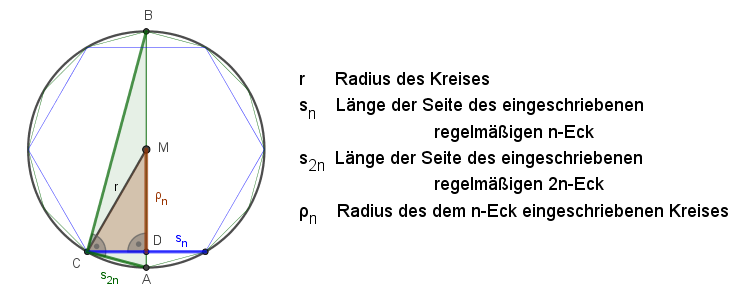
Herleitung
In den Dreieck CDM gilt:
Weiters gilt in dem Dreieck ABC (Kathetensatz):
Für r = 1 folgt:
Mit Hilfe dieser Formel kann eine Tabellenkalkulation aufgebaut werden, um eine untere Schranke für die Zahl Pi zu berechnen.
Mit dem obigen Applet kann also eine untere Schranke für die Zahl Pi berechnet werden. Auf analoge Art kann durch ein umschriebenes n-Eck auch eine obere Schranke für Pi berechnet werden.
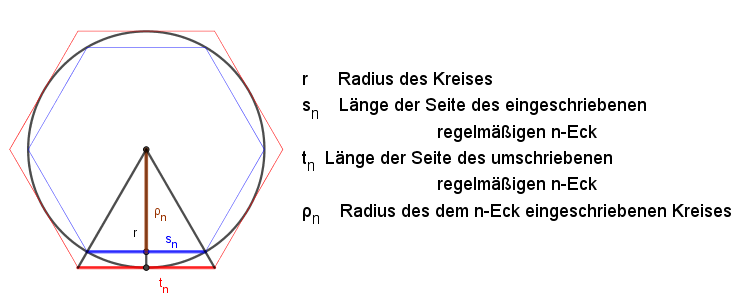
In der obigen Abbildung kann man erkennen (Strahlensatz:
Mit dieser Formel kannst du schrittweise der Umfang U des umschriebenen Vielecks berechnen und somit obere Schranken für Pi bestimmen.
Zur Berechnung von Pi
Aus den Berechnungen weiter oben wissen wir für den Fall r = 1:
und bzw. .
Damit kann folgende Tabelle erstellt werden:
(Laub, J. et al. (1977): Lehrbuch der Mathematik. 2. Band. Arbeitsbuch für die 6. Klasse. Wien: hpt.)
| n | | |
| 6 | 1 | |
| 12 | | |
| 24 | | |
| 48 | ||
| ... | ... | ... |
| 384 | ... | |
| ... | ... | ... |
| | | mit k Wurzelzeichen (k>1) |