Bedeutung höherer Ableitungen
Bisher ist bekannt, dass die 1. Ableitung einer Funktion Auskunft gibt über die Steigung des Graphen der Funktion
Die Ableitungsfunktion ist im Normalfall wieder eine Funktion und kann
somit auch selbst wieder
abgeleitet werden.
Ein Beispiel:
Die Funktion sieht so aus:
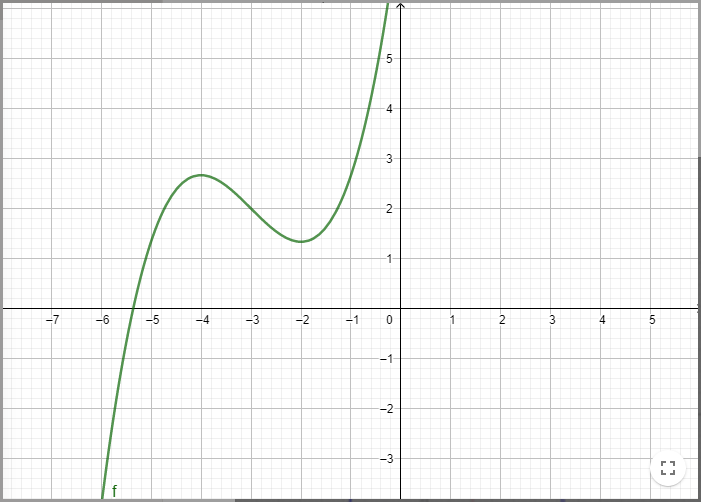
Dann ist die Ableitung und sieht so aus:
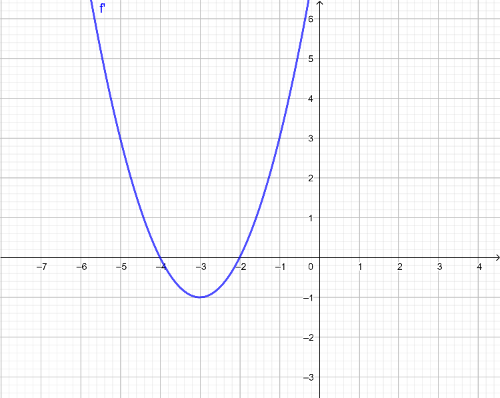
Dieser Graph sieht wie eine ganz normale Funktion aus. Dass es die 1. Ableitung einer anderen Funktion ist, sieht man ihr nicht an.
Diese Funktion kann man ganz normal ableiten. Diese Ableitung heisst "Zweite Ableitung von f".
Sie ist
Der Graph dieser 2. Ableitung sieht so aus:
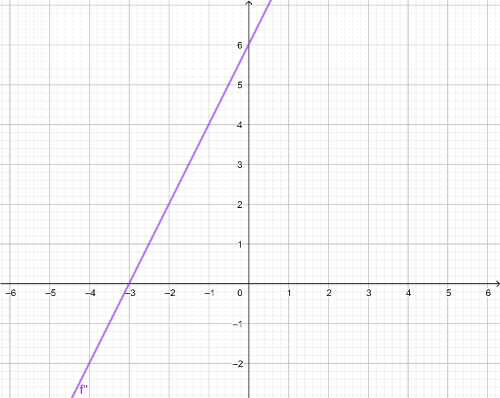
Dieser Vorgang kann weitergeführt werden und man kann je nach Funktion die 3., 4., 5. usw. Ableitung berechnen.
Die Frage ist nun, was diese höheren Ableitung - und insbesondere die 2. Ableitung - für eine Bedeutung haben.
Beantworte dazu die Fragen und nutze die Geogebra-Animation.
Wie viele Punkte gibt es auf dem Graphen von , bei denen die 1. Ableitung ist? (Beantworte die Frage, ohne anzuzeigen und überprüfe danach Deine Antwort.)
Bei welchen der folgenden Punkte auf ist ?
Bei welchen Punkten auf hat die 1. Ableitung ein lokales Maximum oder ein lokales Minimum?
Blende nun die 2. Ableitung ein. Welchen Wert nimmt die 2. Ableitung bei den Punkten ein, die du in Frage 3 ausgewählt hast?
Der Punkt ist ein lokales Minimum der Funktion . Welche der folgenden Aussagen sind richtig.