Inhalt des geogebra-books
| Diese Aktivität ist eine Seite des geogebra-books Elliptische Funktionen & Bizirkulare Quartiken & ... (05.02.2023) |
Elliptische Funktionen sind meromorphe doppelt-periodische komplexe Funktionen,
welche einer komplexen Differentialgleichung des Typs
- mit
Elliptische Funktionen und Kreisbüschel
Die Kreise eines elliptischen Kreisbüschels sind Lösungskurven der Differentialgleichung ,
wobei die Brennpunkte die Grundpunkte des Kreisbüschels sind.
Die Differentialgleichung beschreibt ein parabolisches Kreisbüschel mit als Berührpunkt.
Jede elliptische Differentialgleichung des obigen Typs läßt sich als "Produkt" zweier Kreisbüschel-Differentialgleichungen
auffassen, je nach Lage der Brennpunkte sogar auf verschiedene Arten.
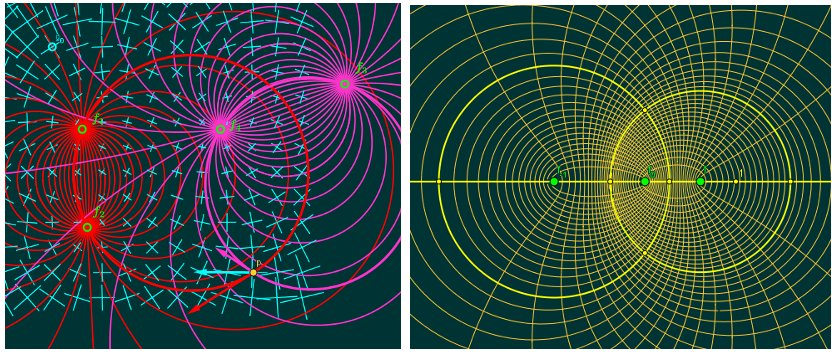
Die Lösungskurven der elliptischen Differentialgleichung sind Winkelhalbierende der sich schneidenden Kreise
aus den 2 Kreisbüscheln des Produkts. Dies ist auch dann der Fall, wenn Brennpunkte zusammenfallen.
Das Bild links oben stellt das elliptische Richtungsfeld dar, das sich als Winkelhabierenden-Feld zweier Kreisbüschel ergibt.
Hinweis: Für 2 komplexe Zahlen ist Winkelhalbierende!
Brennpunkte in Normalform
elliptische Funktionen und bizirkulare Quartiken
Ist die absolute Invariante der 4 Brennpunkte einer elliptischen Differentialgleichung reell,
oder fallen Brennpunkte zusammen, so sind für geeignetes konfokale bizirkulare Quartiken
Lösungskurven der Differentialgleichung.
Sind die 4 Brennpunkte verschieden, so sind
für sind die Brennpunkte konzyklisch, die Quartiken sind 2-teilig;
für liegen 2 der Brennpunkt-Paare spiegelbildlich auf 2 orthogonalen Kreisen, die Quartiken sind 1-teilig.
Konfokale bizirkulare Quartiken: die 4 Typen in Normalform
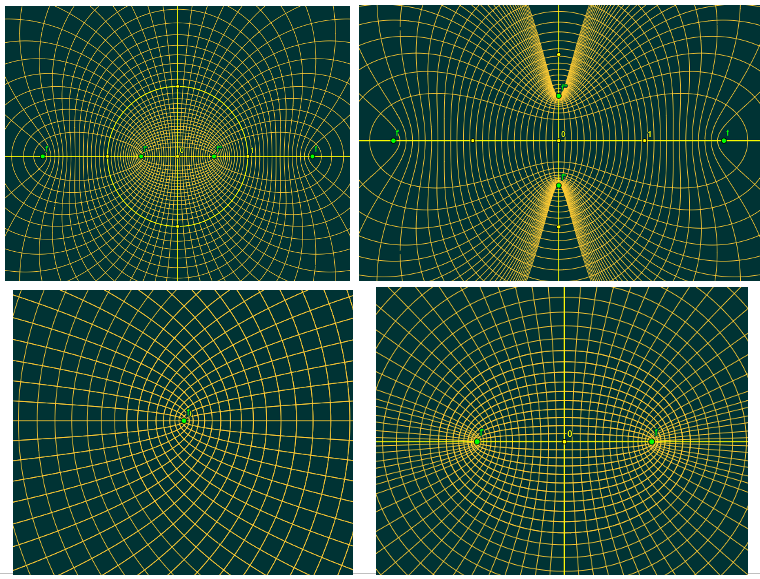
Fallen 2 der Brennpunkte in einen zusammen, und transformiert man diesen nach ,
so ergeben sich konfokale Mittelpunktskegelschnitte.
Fallen 3 Brennpunkte in einem zusammen, so erhält man mit diesem als
konfokale Parabeln.
Oben nicht erfaßt sind 2 Spezialfälle:
- 4 verschiedene Brennpunkte mit : die Brennpunkte sind konzyklisch und besitzen harmonische Lage, es gibt 2-teilige bizirkulare Lösungkurven und im 45°-Winkel dazu 1-teilige bizirkulare Lösungskurven Quadratischer Fall mit Diagonalen.
- hexagonaler Fall: Auf der Möbiuskugel kann man die Brennpunkte als Ecken eines regelmäßigen Tetraeders anordnen. Durch jeden Punkt (von den Brennpunkten abgesehen) gehen sechs 1-teilige bizirkulare Quartiken als Lösungskurven; Schnittwinkel: Vielfache von 60°
6-Eck-Netze ?
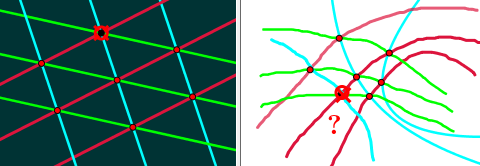
6-Eck-Netze aus Kreisen und bizirkulare Quartiken
W. BLASCHKE's Problem: (1938)
- Man bestimme alle 6-Eck-Netze, die sich aus 3 Kreisscharen bilden lassen!
6-Eck-Netz aus Kreisen: bekannt - - - - - - - neu und unbekannt
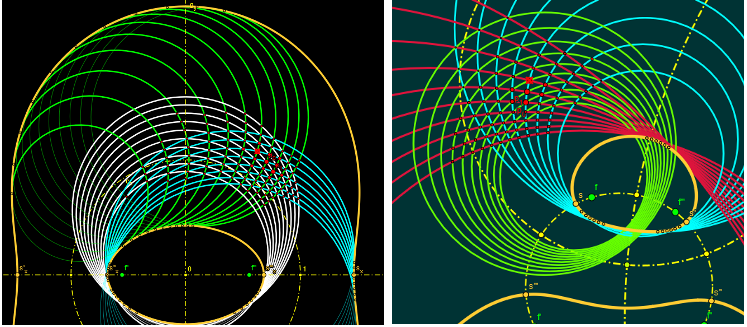
Links: Hommage á WALTER WUNDERLICH. 1938 hat Walter Wunderlich 2-teilige bizirkulare Quartiken untersucht und
gezeigt, dass diese Quartiken 3 Scharen von doppelt-berührenden Kreisen besitzen,
aus denen ein "besonderes Dreiecksnetz aus Kreisen" konstruiert werden kann.
Zu jeder dieser 3 Kreis-Scharen gehört ein Symmetrie-Kreis.
Die 2-teiligen bizirkularen Quartiken besitzen 4 paarweise orthogonale Symmetrie-Kreise.
Die Konstruktion dieser 6-Eck-Netze nutzt die Brennpunkte und die zugeörigen Leitkreise.
Die Konstruktionen sind bei der Suche nach 6-Eck-Netzen aus Kreisen auch erfolgreich bei Mittelpunkts-Kegelschnitten
und deren doppelt-berührenden Kreisen, zu denen auch die Tangenten gehören: möbiusgeometrisch ist ein
doppelt-zählender Brennpunkt und ein Kurven-Punkt!
2013 hat FEDOR NILOV neue 6-Eck-Netze aus Kreisen ( "NEW EXAMPLES OF HEXAGONAl WEBS OF CIRCLES") vorgestellt:
Diese Beispiele beziehen für Kegelschnitte neben den doppelt-berührenden Kreisen auch die zu den Brennpunkten
gehörenden Kreis-Büschel mit ein.
Wir werden im letzten Kapitel dieses geogebra-books eine allgemeine Übersicht über 6-Eck-Netze aus Kreisen vorstellen.
Enthalten sind einige Kreisnetze, die wahrscheinlich bisher unbekannt sind wie das oben rechts angezeigte 6-Eck-Netz.
Die Beispiele von FEDOR NILOV sind als Spezialfälle enthalten.