Veranschaulichung von linearen Funktionen
Teil A (Eigenschaften linearer Funktionen)
Beantworte die folgenden Fragen mithilfe des Handouts.
Welche Form hat jede Funktionsgleichung einer linearen Funktion?
Was gibt der Parameter m in der Gleichung von Aufgabe 1 an?
Was gibt der Parameter n in der Gleichung von Aufgabe 1 an?
Teil B (Zeichnen von linearen Funktionen)
Gegeben sei die Funktion .
a) Vervollständige zunächst die unten abgebildete Wertetabelle.
b) Trage anschließend die Punkte in das Koordinatensystem ein und zeichne eine
Gerade durch die Punkte.
c) Gib eine zu f(x) senkrecht verlaufende Funktion g(x) an.
Hinweis 1: Benutze das Handout!
Hinweis 2: Um g(x) zu finden darfst du das Koordinatensystem aus b) nutzen.
Teil C (Ablesen von linearen Funktionen)
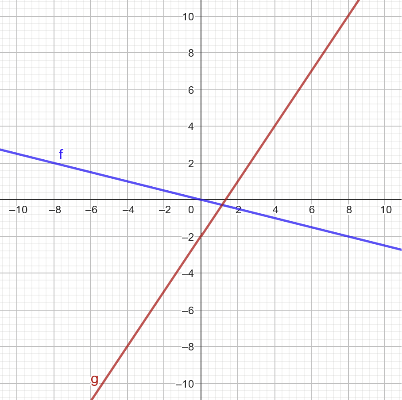
Mit welcher Funktionsgleichung können die beiden Funktionsgraphen beschrieben werden?
Teil D (Funktionseigenschaften)
Gegeben sei der folgende Graph einer Funktion:
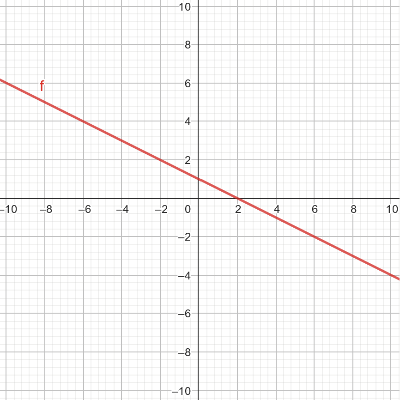
Teil E (Nullstellen)
Übernimm die folgenden Funktionsgleichungen in deinen Hefter und bestimme die Nullstelle!
Du kannst dein Ergebnis überprüfen, indem du deine Lösung in das Eingabefeld eintippst.
Hinweis: Im Handout wird die Berechnung von Nullstellen anhand eines Beispiels erklärt.
Teil F (Bestimmung von Funktionsgleichungen)
Löse die folgenden Aufgaben in deinem Hefter.
Deine Ergebnisse kannst du überprüfen, indem du diese in die entsprechenen Eingabefelder eingibst.
Hinweis: Beachte die im Handout vorgestellten Varianten zur Bestimmung einer Funktionsgleichung.
Teil F - Variante 2
Eine Gerade verläuft durch den Punkt A(5|-24) und hat den Steigungsfaktor m = -6.
Ermittle den y-Achsenabschnitt n und die Funktionsgleichung von g.
Teil F - Variante 3
Die Punkte A(-2|6) und B(4|-24) bestimmen die Gerade g.
Ermittle den Anstieg m, den y-Achsenabschnitt n und die Funktionsgleichung von g.