Теоретичні відомості про особливості застосування функції Sequence
Функція Послідовність в GeoGebra за своїм принципом дії аналогічна циклічному алгоритму в мовах
програмування, але її аргументами і результатами можуть бути безпосередньо
геометричні об'єкти. Це одна з команд, яка працює зі списками (List), які аналогічні
одновимірному масиву у програмуванні. Формат звертання до функції Послідовність:
Послідовність [<Вираз>,<Змінна>, <Початкове значення>, <Кінцеве значення>,
<Крок>]. Така функція повертає список об'єктів,
створених зазначеним виразом і змінною, яка варіюється від початкового до
кінцевого значення з урахуванням вказаного кроку (атрибут кроку можна не
вказувати, тоді він за замовчуванням буде дорівнювати одиниці).
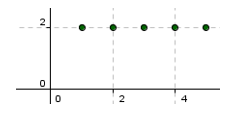
Наприклад, функція Points = Послідовність[(i, 2), i, 1, 5, 1] згенерує список під назвою
«Points», що складається з п'яти точок, координати по осі Ох яких варіюються від 1 до 5.
Аргументи початкового та кінцевого значень можуть бути замінені динамічними змінними, і для них можна створити слайдери. Так, якщо замінити кінцеве значення у виразі цілочисельною
змінною слайдера b (0;10):
Points = Послідовність [(i, 2), i, 1, b, 1]
В результаті кількість згенерованих послідовністю точок у списку буде динамічно змінюватися зі
значенням слайдера b, від 0 до 10 в загальній кількості.
Навчальне дослідження 1. Відредагуйте попередню послідовність так, щоб вона генерувала точки кожні 0,5 кроку по осі Ох. Яка максимальна кількість точок може вийти в списку?
Можна створювати послідовності, використовуючи елементи вже згенерованого
списку об'єктів. Щоб звернутися до окремого елементу списку, є спеціальна функція
Елемент[<Список>, <Номер елемента>].
Наприклад, звернення до третьої точки списку Points буде виглядати так:
Елемент [Points, 3]
Примітка:
в командному рядку можна вказати новий список, вручну перерахувавши його
елементи. Наприклад, список точок: List:{A,B,C} або список чисел: List:{4,34,76,8}.
За допомогою функції Послідовність у комбінації з іншими
командами і функціями в GeoGebra можна створювати складні динамічні побудови,
які можуть не тільки застосовуватися в геометричних дослідженнях, а й приносити
естетичне задоволення. Кілька таких побудов покроково описані нижче.