Lusta/hanyag pénztáros (7.)
A probléma:
Egy moziban a jegyek egységesen 1000 forintba kerülnek. A lusta/hanyag pénztáros nem törődik azzal, hogy felkészüljön a munkájára, így váltópénz nélkül kezdi a napot. Nyitáskor hosszú sor áll az ablak előtt, mindenkinél egy darab kétezres vagy egy darab ezres van véletlenszerű eloszlásban, és mindenki egy darab jegyet akar venni. Várhatóan hány embert tud kiszolgálni a pénztáros?
Vizsgáljuk egy GeoGebrás modellen a problémát! Szerezzünk tapasztalatokat!
Ha többféle eszközzel szimuláljuk ezt a véletlen jelenséget, és várjuk, hogy a kiszolgált vásárlók számának átlaga egy jól meghatározott szám körül fog ingadozni, nagy eséllyel csalódni fogunk, ez nem következik be. Ebből következően feléledhet a gyanú, hogy ennek a valószínűségi változónak nincs is várhatóértéke. Indokolt tehát a matematikai vizsgálat.
Először megadjuk a problémát leíró valószínűségi változó eloszlását! (Lásd Catalan számok!)
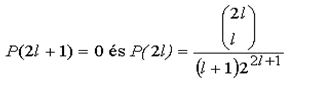
Ha lenne a valószínűségi változónak várhatóértéke, akkor az alábbi sor összege lenne az.
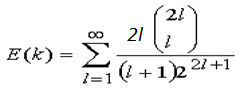
A sor összegét kereső GeoGebra CAS fájl
A GeoGebra is azt sejteti, hogy a sor divergens. Következzen itt egy hagyományos maatematikai bizonyítás a "sorok professzorától":
Dr Németh József tanár úr bizonyítása
