Une fonction bien connue ....

Voici l'objectif ! Mais n'allons pas trop vite !

Notre plan géogébra

Consignes

Dans le plan au dessus, placer le point A sur l'origine du repère et le point B(1;0). Créer un curseur a représentant un nombre décimal pouvant évoluer entre 0 et 10. Dans le champ de saisir entrer la commande Point(Cercle(B, a )) pour créer un point mobile C sur l'axe des abscisses situé à la distance a de C. Ensuite créer un demi-cercle entre A et C. Tracer la perpendiculaire en B à l'axe des abscisses ; puis par l'outil intersection obtenez l'intersection D de cette perpendiculaire avec le demi-cercle. Tracer la parallèle à l'axe des abscisses passant par D, et utiliser l'outil intersection pour obtenir l'autre intersection E avec le demi-cercle.

Le point E

Clairement l'ordonnée de E est la même que celle de D. Mais qu'elle est l'abscisse de E en fonction de défini dans l'énoncé ( correspond au a du curseur) ?

Première conjecture ?

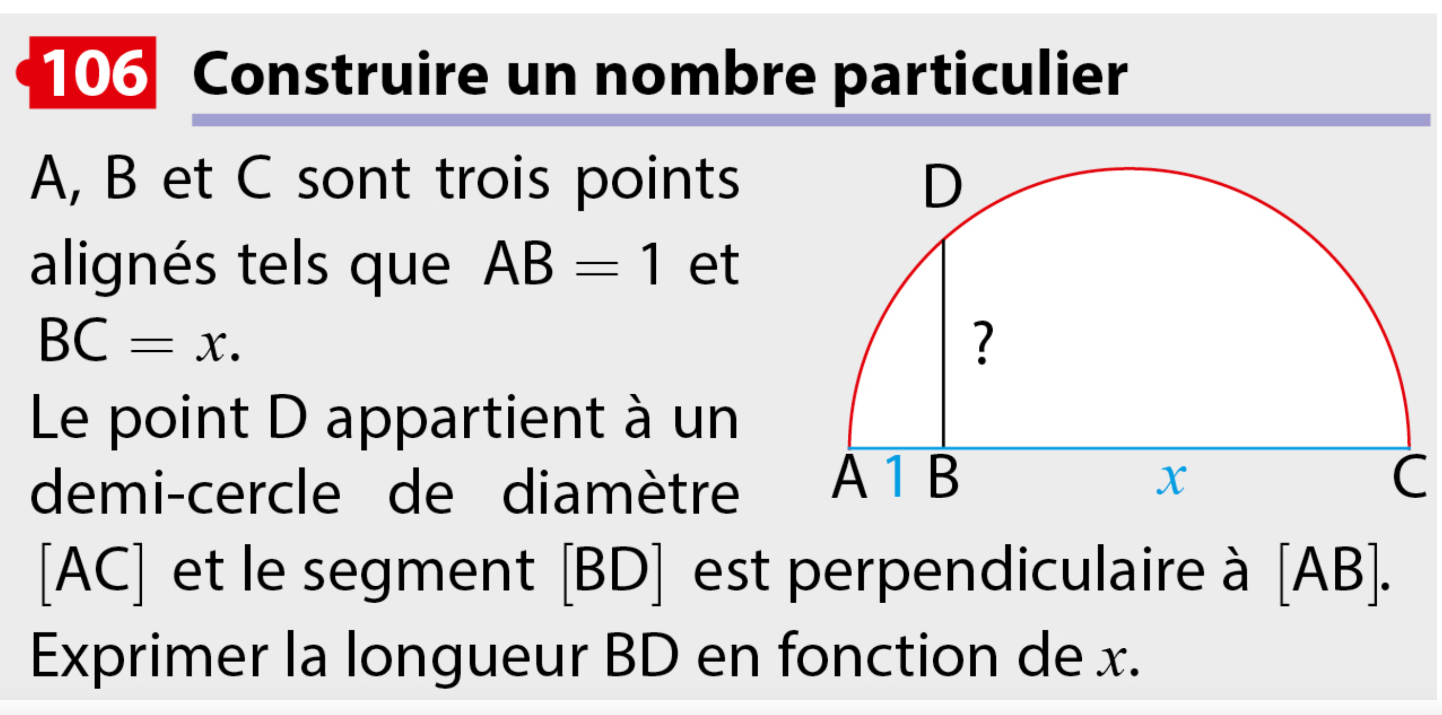
Dans un premier temps, essayer de faire varier le curseur et faite apparaitre la longueur BD avec l'outil de mesure de longueur. De même faire apparaitre la longueur BC. A ce stade, ceux qui devine la relation entre BC et BD l'inscrivent ici:

Tracer le déplacement du point E

Faire un clic droit sur le point E, et choisissez de faire apparaître la trace du point E. Faire varier le curseur a de façon à obtenir un beau tracé du point mobile E. Conjecturer la fonction qui permet d'exprimer la longueur BD en fonction de x=BC ?

Démonstration de la conjecture

Il faut maintenant écrire la démonstration de cette conjecture. Il faut en particulier utiliser des connaissances en géométrie de collège. Bon courage ! Recopier la démonstration .