Outline
₇3d shapes:Construction polyhedra. Coloring edges and faces
*From Book: Extended definitions of point location estimates https://www.geogebra.org/m/hhmfbvde
From: List of My Public Books on GeoGebra Topics: Constructing polyhedra -https://www.geogebra.org/m/eabstecp
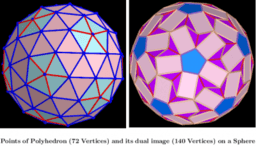
Table of Contents
Construction polyhedra
- 1. The problem of extreme distribution of points on the surface of a sphere.
- 2. Generating Elements of mesh modeling the surfaces of convex polyhedrons and its dual images
- 3. Vertices n=24. Coloring the edges and faces of a polyhedron and its dual image.
- 3 in 1. Constructing, surface triangulation, visualizing polyhedron. New Version.
- Images. Constructing, surface triangulation, visualizing polyhedron
- Images. n=4: Tetrahedron -Platonic Solid and n=5: Triangular bipyramid (Triangular Dipyramid) -Johnson solid J₁₂ and their Dual Polyhedrons
- Images. n=6: Octahedron -Platonic Solid and n=8: Square antiprism and their Dual Polyhedrons
- Images. n=12: Icosahedron -Platonic Solid and n=20. Their Dual Polyhedrons
- Images. n=16: Two polyhedra with the same number of vertices but different extreme distributions on the described sphere
- Images. n=24: Biscribed Snub Cube (laevo) and n=32. Their Dual Polyhedrons
- Example of non-uniqueness of the extreme distribution of n=16 particles on the surface of a sphere.
- 3d shapes: n=72. Extreme distribution of points on the surface of a sphere and comparison with two known but not extreme ones having the same number of vertices
- Coloring of edges and faces of a polyhedron(n=72) extreme distribution and its dual image.
- Biscribed Pentakis Snub Dodecahedron (V=72) and its dual image: Coloring the edges and faces
- Coloring the edges and faces of a polyhedron(n=72) Pentakis Snub Dodecahedron (laevo) and its dual image.
Coloring edges and faces
- Images. n=4: Tetrahedron -Platonic Solid and n=5: Triangular bipyramid (Triangular Dipyramid) -Johnson solid J₁₂ and their Dual Polyhedrons
- Images. n=6: Octahedron -Platonic Solid and n=8: Square antiprism and their Dual Polyhedrons
- Images. n=12: Icosahedron -Platonic Solid and n=20. Their Dual Polyhedrons
- Copy of 3 in 1. Constructing, surface triangulation, visualizing polyhedron. New Version.
- Truncated Tetrahedron, n=12. Polyhedra with extreme distribution of equivalent vertices.
- Example of non-uniqueness of the extreme distribution of n=16 particles on the surface of a sphere.
- Truncated Cube, n=24. Polyhedra with extreme distribution of equivalent vertices.
- 3. Vertices n=24. Coloring the edges and faces of a polyhedron and its dual image.
- Images. n=24: Biscribed Snub Cube (laevo) and n=32. Their Dual Polyhedrons
- Biscribed Truncated Octahedron, n=24. Polyhedra with extreme distribution of equivalent vertices.
- Icosidodecahedron, n=30. Polyhedra with extreme distribution of equivalent vertices.
- Pentakis Dodecahedron(V=32) and its dual image -Truncated Icosahedron(V=60): Coloring the edges and faces
- Truncated Dodecahedron, n=60. Polyhedra with extreme distribution of equivalent vertices.
- Rhombicosidodecahedron-c(V=60) and its dual image - Deltoidal Hexecontahedron(V=62): Coloring the edges and faces
- Biscribed Truncated Icosahedron, n=60. Polyhedra with extreme distribution of equivalent vertices.
- Rhombicosidodecahedron, n=60. Polyhedra with extreme distribution of equivalent vertices.
- Biscribed Snub Dodecahedron, n=60. Polyhedra with extreme distribution of equivalent vertices.
- Coloring the edges and faces of a polyhedron(n=72) Pentakis Snub Dodecahedron (laevo) and its dual image.
- Biscribed Pentakis Snub Dodecahedron (V=72) and its dual image: Coloring the edges and faces
- Coloring of edges and faces of a polyhedron(n=72) extreme distribution and its dual image.
- Rectified truncated icosahedron(V=90) and its dual image: Coloring the edges and faces
- Biscribed Truncated Icosidodecahedron, n=120. Polyhedra with extreme distribution of equivalent vertices.
- Finding and coloring edges and faces of a polyhedron and its dual image. V=180
- Canonical Truncated Snub Cube (laevo)(V=120) and its dual image: Coloring the edges and faces
- Images: Canonical Truncated Snub Cube (laevo)(V=120) and its dual image: Coloring the edges and faces
- Canonical Truncated Snub Cube (laevo)(V=120) and its dual image: Coloring the edges and faces
- Biscribed Hexpropello Dodecahedron (dextro) (V=140) and its dual image: Coloring the edges and faces
- Biscribed Orthotruncated Propello Icosahedron (V=120) and its dual image: Coloring the edges and faces
- Rhombicosidodecahedron from Biscribed Pentakis Dodecahedron for the case of trisection of its 1st-order segments
- Truncated Dodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 2nd-order segments
- Truncated Icosahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 3rd-order segments
- Truncated icosidodecahedron (V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 4th-order segments
- Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 5th-order segments
- Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 6th-order segments
- The Great Rhombicosidodecahedron (V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 7th-order segments
- Rhombicosidodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 8th-order segments(Variant1)
- Rhombicosidodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 9th-order segments(Variant2)
- Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of a trisection of its 10th-order segments
- Biscribed Pentakis Dodecahedron (V=32) from Biscribed Pentakis Dodecahedron for the case of a trisection of its 11th-order segments