Problema del puente de Königsberg
En la ciudad de Königsberg, Prussia (1736), hoy Kaliningrado Rusia, el Río Pregel fluía a través de la ciudad dividiéndola en 4 regiones de tierra: 7 puentes atravesaban el río en diferentes ubicaciones. El siguiente mapa muestra el mapa de Königsberg donde las 4 regiones de tierra son A, B, C, D y los puentes son a, b, c, d, e, f y g.
Instrucciones
Dibuja en la siguiente imagen cómo resolverías el problema de los puentes de Königsberg.
Responde la siguiente pregunta:
¿Es posible caminar por Königsberg cruzando cada uno de sus siete puentes exactamente solo una vez?
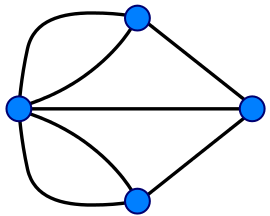
El matemático suizo, Euler, determinó que los puntos intermedios de un recorrido posible necesariamente han de estar conectados a un número par de líneas. En efecto, si llegamos a un punto desde alguna línea, entonces el único modo de salir de ese punto es por una línea diferente. Esto significa que tanto el punto inicial como el final serían los únicos que podrían estar conectados con un número impar de líneas. Sin embargo, el requisito adicional del problema dice que el punto inicial debe ser igual al final, por lo que no podría existir ningún punto conectado con un número impar de líneas.
En particular, como en este diagrama los cuatro puntos poseen un número impar de líneas incidentes (tres de ellos inciden en tres líneas, y el restante incide en cinco), entonces se concluye que es imposible definir un camino con las características buscadas que son los 7 puentes de Königsberg.