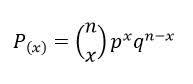DEFINICIÓN
Una distribución binomial, en estadística, es una distribución de probabilidad discreta (función que asigna a cada suceso definido sobre la variable la probabilidad de que dicho suceso ocurra) que describe el número de éxitos al realizar n experimentos o ensayos de Bernoulli independientes entre sí, acerca de una variable aleatoria.
Un experimento de Bernoulli se caracteriza por tener solo dos resultados. Uno de ellos se denomina «éxito» y al otro, «fracaso». Por ejemplo, imagínate el lanzamiento de una moneda cuyo resultado de «sacar cara» es el éxito. Si lanzamos 5 veces la moneda y contamos los éxitos que obtenemos, nuestra distribución de probabilidades se ajustaría a una distribución binomial.
En la distribución binomial tenemos tres variables:
- n es el número de veces que repetimos el experimento.
- p es uno de los dos resultados al que llamaremos éxito.
- q es el otro resultado posible al que llamaremos fracaso.
FÓRMULA