1.3 Tetraedros
- Um tetraedro é uma pirâmide triangular.
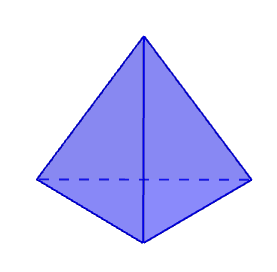
Planificação:
Geometria molecular: tetraédrica
A geometria molecular explica como estão dispostos os átomos dentro de uma molécula. Os átomos tendem a ficar na posição mais espaçada possível. Assim, conseguem adquirir estabilidade. As moléculas com estruturas tetraédricas, possuem elementos centrais, por exemplo:
Metano
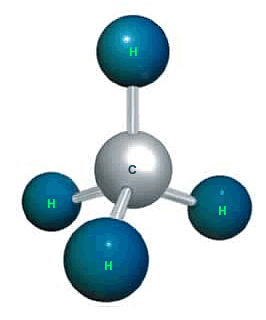
Tetraedro regular:
- Suas faces são determinadas por quatro triângulos equiláteros.
- Possui 4 vértices e 6 arestas.
Seção paralela à base de um tetraedro
Ao determinarmos uma seção (região poligonal plana com um vértice em cada aresta) em uma pirâmide triangular, temos que:
- as arestas laterais e a altura ficam divididas na mesma razão.
- a seção e a base são triângulos semelhantes.
- a razão entre as áreas da seção e da base é igual ao quadrado da razão de suas distâncias ao vértice.
Exercícios:
05) Considerando uma pirâmide de base quadrada cujas arestas laterais tenham a mesma medida que as da base e um tetraedro regular com arestas congruentes a da pirâmide, quantos vértices, faces e arestas terá o sólido formado pela junção das faces laterais dessas pirâmides?
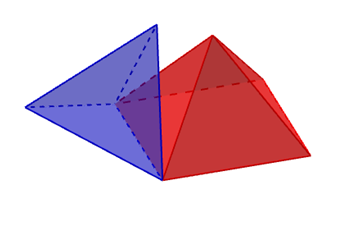
Resolução: questão 5
Esferas Inscrita e Circunscrita a um Tetraedro:
06) O ponto 'O' centro tanto da esfera inscrita quanto da circunscrita, em relação ao triângulo AEB, pode ser considerado:
a)Incentro
b)Circuncentro
c)Ortocentro
d)Epicentro
e)Baricentro
f) Hipocentro
Uma esfera é circunscrita a um tetraedro regular ABCD quando toca todos os pontos que o definem (A,B,C e D) e é inscrita ao mesmo quando tangencia todas as suas faces.
Considerando E o ponto médio entre C e D no tetraedro ABCD, observe o triângulo isósceles AEB:
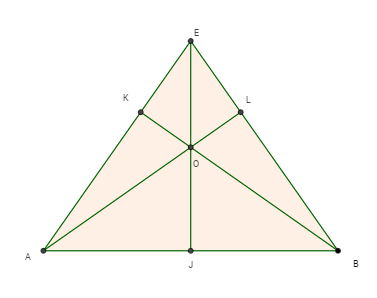
07) Os raios das esferas circunscrita e inscrita ao tetraedro tem respectivamente o mesmo comprimento que os segmentos:
a)JO e EL
b)AO e OK
c)BO e LA
d)EA e LO
e)LO e BO