SEQUÊNCIA: FRAÇÕES
Você já viu uma receita de bolo?
Veja a lista de ingredientes de um bolo de chocolate fofinho:

___________________________________________________________________________________________
Nessa lista, algumas quantidades são representadas por números diferentes daqueles que contam quantidades inteiras:
Para entendermos essas quantidades, precisamos conhecer o conceito de fração.
________________________________________________________________________________
Fração
Uma fração é a representação de uma ou mais partes de uma quantidade que foi dividida em partes iguais.
Calma, vamos explicar melhor ...
Pense em uma quantidade. Essa quantidade pode ser representada por um retângulo, ou seja, a quantidade total pensada é representado pelo retângulo todo:

Imagine agora que queremos apenas uma parte dessa quantidade: Vamos dividir o retângulo em 3 partes iguais e usar 1 pedaço:

Essa parte destacada é uma fração do retângulo, ou seja, uma fração da quantidade representada.
_______________________________________________________________________________________
Escrevendo uma fração
Uma fração é escrita da seguinte maneira:
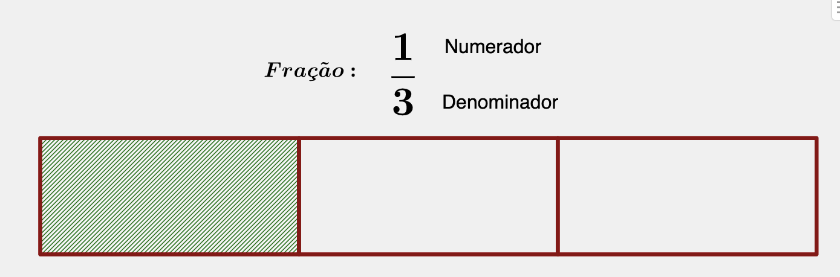
- O Denominador representa o número que dividiu a quantidade total em partes iguais.
- O Numerador representa o número de partes iguais que queremos representar na fração.
Voltando à receita de bolo de chocolate, queremos de uma xícara de amido de milho.
Podemos chegar a essa quantidade dividindo a xícara em 4 partes iguais (denominador) e usar 3 dessas partes (numerador).
Veja algumas representações da fração :


________________________________________________________________________________________________________
Use o aplicativo abaixo e explore algumas frações e suas representações. Altere os valores do denominador e do numerador usando os controles.
(Para usar o modo tela cheia, clique no ícone no canto inferior direito.)
_______________________________________________________________________________________
Lendo uma fração
A leitura de uma fração segue algumas regrinhas:
- O numerador é lido como um número cardinal: Um, dois, três, quatro, ...
- O denominador, quando entre 2 e 10, é lido como ordinal: Terço, quarto, quinto, sexto, sétimo, oitavo e nono.
Veja alguns exemplos:
dois terços
cinco sétimos
quatro nonos
- Quando o denominador é maior que 10, lemos o número cardinal seguido da palavra avos.
Exemplos:
cinco doze avos
doze dezessete avos
- o denominador 2 é lido como "meio(s)".
um meio (ou simplesmente "meio")
cinco meios
- Os denominadores múltiplos de 10 são lidos:
um décimo
um centésimo
um milésimo
etc.
_______________________________________________________________________________________
Calculando a fração de uma quantidade
Usando o que aprendemos até agora, podemos calcular a fração de uma determinada quantidade. O raciocínio segue a mesma lógica...
Para exemplificar, vamos resolver um probleminha:
_______________________
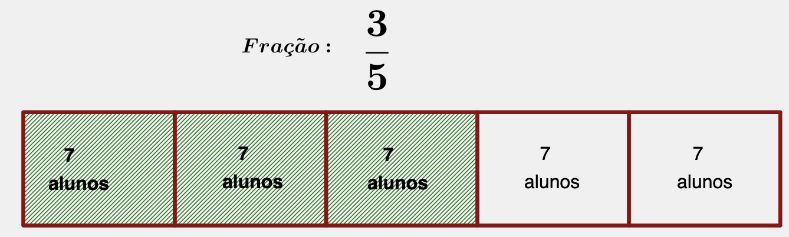
Uma determinada turma do 6o ano possui 35 alunos. Nessa turma, dos alunos preferem o console Xbox series s ao console Playstation4.
Qual a quantidade de alunos que preferem o console Xbox series s nessa turma?
 _______________________
_______________________
Para encontrar a solução desse problema, precisamos saber quanto é de 35.
Sabemos que o denominador representa o número pelo qual o valor total foi dividido.
Sabemos também que o numerador é a quantidade de partes dessa divisão que queremos.
Então,
Calculamos a fração de uma quantidade dividindo essa quantidade pelo denominador e multiplicando o numerador pelo resultado da divisão.
Mãos à obra!

Concluímos que de 35 é igual a 21.
Nessa turma de 6o ano, 21 alunos preferem o console Xbox series s ao console Playstation 4.
Podemos representar essa fração da seguinte maneira:


_______________________________________________________________________________________
Vamos praticar um pouco!
(Para usar o modo tela cheia, clique no ícone no canto inferior direito.)
_______________________________________________________________________________________
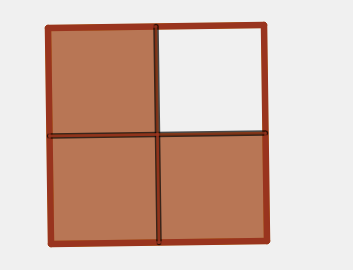
Frações equivalentes
Podemos representar uma mesma quantidade com frações diferentes.
veja o exemplo:
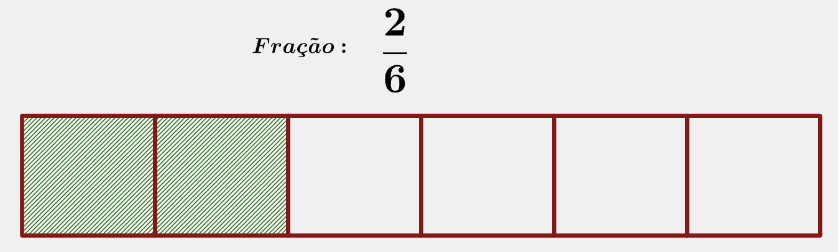

Nesse exemplo, dizer que 2/6 é igual a 1/3 significa dizer que "2 partes de 6" é a mesma quantidade que "1 parte de 3".
A fração mais simples (menor denominador) é chamada de fração irredutível.
Como podemos então encontrar a forma mais simples de uma fração?
1o Passo: Precisamos encontrar um número que consiga dividir tanto o numerador quanto o denominador ao mesmo tempo (com resultados inteiros).
2o Passo: Dividir o numerador e o denominador pelo número encontrado no passo anterior, gerando uma nova fração.
3o Passo: Repetir os dois primeiros passos até não haver mais nenhum número que divida o numerador e o denominador ao mesmo tempo.
Vamos simplificar a fração 12/18 como exemplo:
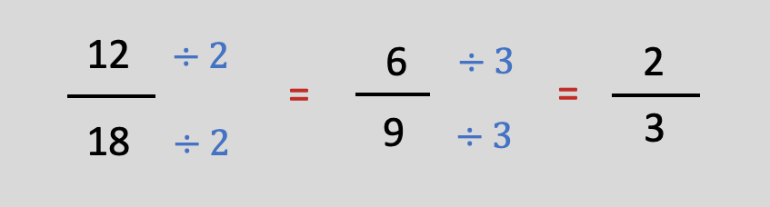
As frações 12/18, 6/9 e 2/3 são equivalentes.
2/3 é uma fração irredutível.
________________________________________________________________________________________________________
Use o aplicativo abaixo e explore algumas frações equivalentes.
(Para usar o modo tela cheia, clique no ícone no canto inferior direito.)