een vleugje goniometrie
Wat is speciaal aan een regelmatige vijfhoek?
Je vindt online een breed assortiment aan websites waar 'de gulden snede' ter sprake komt.
Op sommige wordt aan de regelmatige vijfhoek een speciale status toegekend omdat hier de gulden snede zou voorkomen. Er is duidelijk sprake van een begripsverwarring tussen het getal (of ) en de verdeling van een lijnstuk volgens een middelevenredigheid. Niemand kent een vierkant uitzonderlijke metafysische of esthetische kwaliteiten toe omdat de diagonaal van een vierkant met zijde 1 gelijk is aan .
Evenmin stellen mensen zich vragen bij een gelijkheid als sin 60°= sin = .
Wel, er bestaat een analoge gelijkheid met een worteluitdrukking voor de sinus van = 18°.
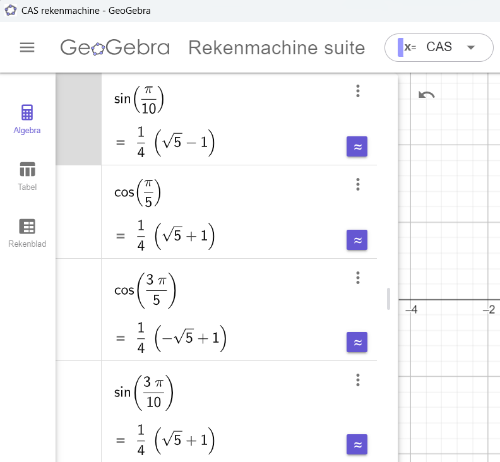
En dus neen, er is niet speciaals aan een regelmatige vijfhoek. Vanuit deze gelijkheid is het logisch dat bij berekeningen in deze figuur het getal (en dus ook ) opduikt.
Je mag dit best pittige bewijs gerust overslaan en enkel de boodschap meenemen dat er niets mysterieus is aan een vijfhoek of een pentagram 'omdat daar de gulden snede zou in voorkomen'.
In volgende pagina's zie je enkele illustraties. Ben je geen wiskundige, dan kan je ook hier de getallen en afleidingen laten voor wat ze zijn. Onthoud gewoon dat het de logica zelf is dat je en terugvindt in meetkundige toepassingen met regelmatige vijf- of tienhoeken.
het verband tussen phi en een hoekgrootte
De gelijkheid is gewoon een wiskundige gelijkheid, net zoals , die je in de lessen goniometrie leert. Dit betekent dat het voor de hand ligt dat je gaat tegenkomen in meetkundige toepassingen waarin hoeken van of veelvouden daarvan tegenkomt. Immers, de lengte van de zijde van een regelmatige n-hoek met straal r is gelijk aan .
Met het commando TekstIrrationaal kan je gemakkelijk andere verwante gelijkheden controleren: