Experiment - Conical Pendulum
Motivation
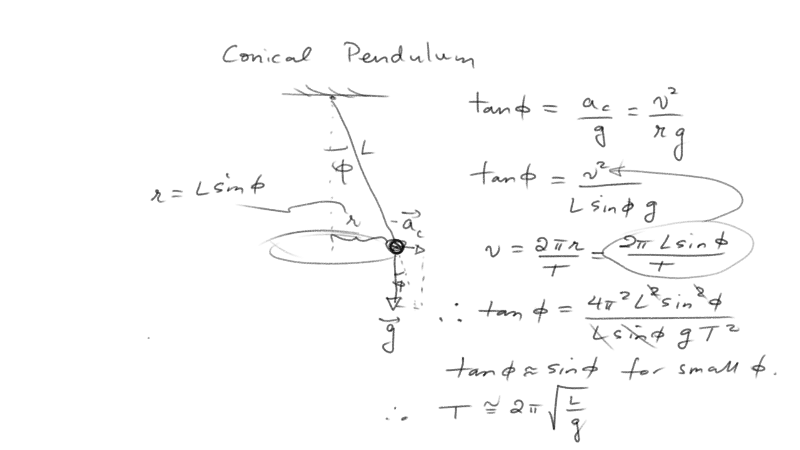
A conical pendulum is one in which the mass swings in circles such that the string to which it is attached traces out a cone every period of the motion.
One way to think of a conical pendulum is to think of it like you would a centrifuge from this chapter. The pendulum feels earth's gravity pulling downward and it feels the added effect of outward gravity due to the inward centripetal acceleration.
In this lab we will investigate whether the shape of the path traced out actually matters, and attempt to calculate the period of the conical (or roughly conical) pendulum by only knowing the length of the string from which it hangs and the gravitational constant.
Procedure
- Set up a mass hanging from a string.
- Measure the distance from the support to the center of mass of the hanging mass. Call this L.
- Give the pendulum a push so that it roughly traces out a circular path as it goes, and then time five periods by hand using your phone or a stopwatch. Divide by five and call this T1 where the subscript denotes the first trial. Measure the period five times while attempting to make the swing similar to the first case.
- Average those values and record the value.
- Now give the pendulum a more careless swing. Don't swing it wildly, but be less concerned about whether it is a perfectly circular path.
- In the same way as in steps 3 and 4 above, calculate the periods and their average. If the pendulum doesn't repeat the same path, measure the period based on the time it takes to go around the support in an angular sense and ignore how far outward it is from center.
- Swing the pendulum in the ordinary (non-conical way) and once again make the same measurement as in steps 3 and 4 above.
Calculations
- Using the result for period in the derivation above, calculate the theoretical period using L and g=9.8m/s2.
- Calculate the percent difference between your measured results and this theoretical one for the three scenarios (circular path, careless path, ordinary pendulum)
Questions
- Does it seem to matter how you swing a pendulum in terms of what its period will be?
- In which case is your result closest to the theoretical value?
- At what angle of swing (in degrees and radians both) should we expect an error greater than 5% based on the approximation used in the derivation?
- When we write , does our choice of angular units matter?