画像圧縮〜少ないデータ量で近似する
0.問題
<演習1>
画像の濃淡を数値であらわすとき、識別力を下げずに次元を下げたい。
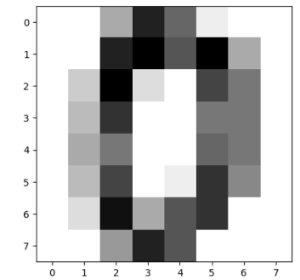
8☓8で「0」を表す画像データ行列を加工して、行列の階数を下げて圧縮の程度を確認しよう。
1.演習1
「0」画像の濃淡を8行8列の行列に表したものをXとする。
この行列を3行列U、S、Vの積に分解するSVD分解をしよう。
すると、Sは対角成分に特異値s1,s2,s3,.....に、他は0になる。UとVが直交行列。
XはΣsiUiVitで近似できる。iはその行列のi列目を切り出した1列の列ベクトルの取り出しです。
X1=s1U1V1t
X2=s1U1V1t+s2U2V2t
X3=s1U1V1t+s2U2V2t+s3U3V3t
。。。。。。。。。
X6 ≒ X
行列のサイズが8であっても、特異値s6まであり、S7=s8=0だとしたら、
X6を求めれば、もとのXとほぼ同じ画像に復元できる。
これを低ランク近似というデータ量がどのくらいへるかを計算してみる。
X1はs1で1個、U1列ベクトルに8個、V1列ベクトルに8個、合計1+8+8=17個
X2は2列目の特異値に対応するデータが追加されて、17*2=34個
X3は3列目の特異値に対応するデータが追加されて、17*3=51個
X4は4列目の特異値に対応するデータが追加されて、17*4=68個
.......
X6は17*6=102個
もとのデータ量は8*8=64個だから、3列目まではデータ節約になる。
もし800*600=48万個のデータでできた画像が、rank100に圧縮できれば、
100(1+800+600)≒14万個のデータで済むので、保持するデータ量の節約になる。
つまり、S,U,Vの行列データを端からすべて保持せず、端から100番目まであれば済むことになる。
<julia>
using LinearAlgebra
x0=[ 0. 0. 5. 13. 9. 1. 0. 0.;
0. 0. 13. 15. 10. 15. 5. 0.;
0. 3. 15. 2. 0. 11. 8. 0.;
0. 4. 12. 0. 0. 8. 8. 0.;
0. 5. 8. 0. 0. 9. 8. 0.;
0. 4. 11. 0. 1. 12. 7. 0.;
0. 2. 14. 5. 10. 12. 0. 0.;
0. 0. 6. 13. 10. 0. 0. 0.]
using PyPlot
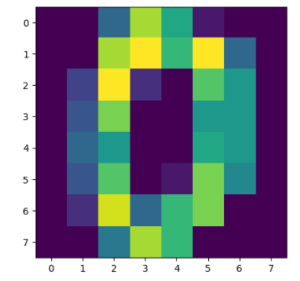
#もとの画像の表示
plt.imshow(x0)
#画像の行列をU,S,Vに分解する。
U,S,V=svd(x0)
#==================================================================
SVD{Float64, Float64, Matrix{Float64}, Vector{Float64}}
U factor:
8×8 Matrix{Float64}:
-0.227147 0.489927 0.275667 … -0.556251 0.0 0.531409
-0.53908 0.273281 0.0188344 0.251859 -0.12505 0.0302385
-0.387732 -0.318589 0.193466 -0.408655 -0.0777116 -0.31044
-0.302179 -0.323856 0.267671 0.557167 -0.134868 0.517763
-0.263389 -0.314291 0.26639 -0.177026 -0.43388 -0.277758
-0.335106 -0.329088 -0.0536914 … -0.100526 0.828133 0.058899
-0.423318 0.0821909 -0.815776 -0.0375244 -0.185262 0.00673247
-0.235119 0.514853 0.274298 0.326904 0.227499 -0.521129
singular values:
8-element Vector{Float64}:
48.30784500260761
24.95585263978704
8.020753260580447
6.029373007622524
3.534479321858529
0.6157632795726049
0.0
0.0
Vt factor:
8×8 Matrix{Float64}:
-0.0 -0.121635 -0.635846 -0.351655 … -0.547891 -0.262225 -0.0
-0.0 -0.199337 -0.182616 0.678604 -0.292419 -0.344252 -0.0
0.0 0.141722 -0.0620057 0.466305 -0.400015 0.690527 0.0
-0.0 -0.289877 -0.598803 0.25419 0.659918 0.108522 -0.0
0.0 -0.707353 0.443133 0.1381 -0.0853768 -0.203097 0.0
0.0 -0.583958 -0.0597936 -0.33869 … -0.107305 0.53186 0.0
0.0 0.0 0.0 0.0 0.0 0.0 1.0
1.0 0.0 0.0 0.0 0.0 0.0 0.0
using LinearAlgebra
using PyPlot
#表示用の関数を作る。kを指定して合計するΣSkUkVkt
function disp(k)
x=sum([s[k]*U[:,k]*transpose(V[:,k]) for k in 1:k])
print("rank",k)
plt.imshow(x)
end
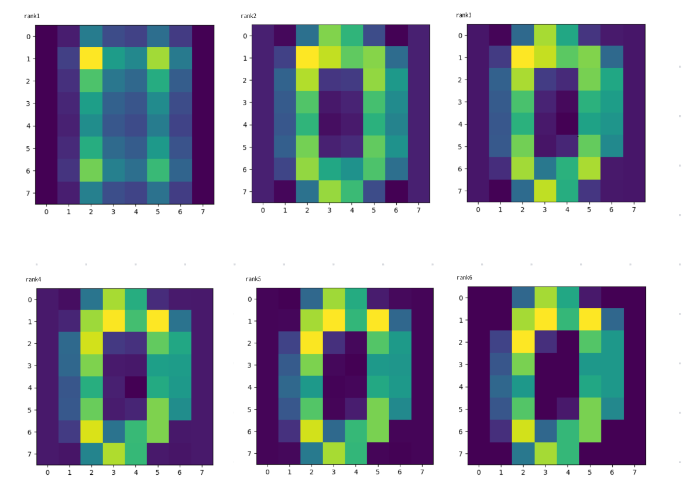
#1つ実行するたびに、1つの画像が表示されます。
disp(1)
disp(2)
......
disp(6)
<Python>
#juliaと同様にできる。
import numpy as np
x0=np.array([[ 0., 0., 5., 13., 9., 1., 0., 0.],
[ 0., 0., 13., 15., 10., 15., 5., 0.],
[ 0., 3., 15., 2., 0., 11., 8., 0.],
[ 0., 4., 12., 0., 0., 8., 8., 0.],
[ 0., 5., 8., 0., 0., 9., 8., 0.],
[ 0., 4., 11., 0., 1., 12., 7., 0.],
[ 0., 2., 14., 5., 10., 12., 0., 0.],
[ 0., 0., 6., 13., 10., 0., 0., 0.]])
import numpy as np
from numpy.linalg import svd
U, S, Vt = svd(x0)
print(U)
print(S)
print(Vt)
#===============================================================
[[-0.22714678 0.48992739 0.27566678 -0.15755125 -0.12550139 -0.55625083 0. 0.53140882]
[-0.53908005 0.27328068 0.01883441 0.71916474 0.19280258 0.25185888 -0.12505044 0.03023848]
[-0.38773218 -0.31858921 0.19346641 -0.20168304 0.63296791 -0.40865501 -0.07771161 -0.31043999]
[-0.30217909 -0.32385608 0.26767054 -0.36448633 0.05103709 0.5571669 -0.1348682 0.51776255]
[-0.26338915 -0.31429094 0.26639012 0.09414371 -0.67474504 -0.1770263 -0.43387994 -0.27775823]
[-0.33510624 -0.32908792 -0.05369139 0.11924292 -0.250848 -0.10052563 0.8281329 0.05889901]
[-0.42331758 0.08219089 -0.81577588 -0.31623618 -0.11303018 -0.03752439 -0.18526211 0.00673247]
[-0.23511864 0.51485336 0.27429832 -0.40170401 -0.11332252 0.32690435 0.22749926 -0.52112878]]
[48.307845 24.95585264 8.02075326 6.02937301 3.53447932 0.61576328 0. 0. ]
[[-0. -0.12163488 -0.63584592 -0.35165517 -0.29714822 -0.54789077 -0.26222547 -0. ]
[-0. -0.19933667 -0.18261557 0.67860378 0.51224488 -0.29241939 -0.34425199 -0. ]
[ 0. 0.14172169 -0.06200574 0.46630482 -0.34898491 -0.40001459 0.69052728 0. ]
[-0. -0.28987701 -0.59880272 0.25418992 -0.21336759 0.65991771 0.10852187 -0. ]
[ 0. -0.70735326 0.44313298 0.13810032 -0.48546381 -0.08537679 -0.20309735 0. ]
[ 0. -0.58395848 -0.05979355 -0.33869034 0.49630315 -0.10730494 0.53185986 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 1. ]
[ 1. 0. 0. 0. 0. 0. 0. 0. ]]
# 取り出したベクトルを1列ベクトルとして整形してから、転置して行列の積を計算する。
from matplotlib import pyplot
def disp(k):
x=sum([S[k]*U[:,k].reshape(8,1)@((Vt[k].reshape(8,1)).transpose()) for k in range(k)])
print("rank",k)
fig, ax = pyplot.subplots()
ax.imshow(x, cmap = 'binary')
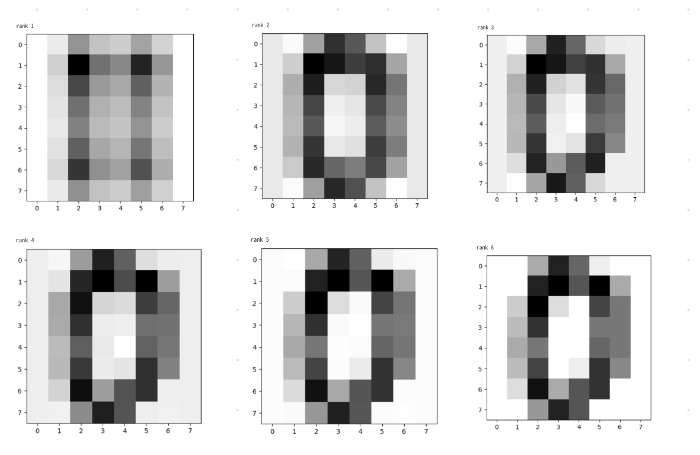
#1つ実行するたびに、1つの画像が表示されます。
disp(1)
disp(2)
....
disp(6)
<geogebra>
x0={{ 0., 0., 5., 13., 9., 1., 0., 0.},
{0., 0., 13., 15., 10., 15., 5., 0.},
{ 0., 3., 15., 2., 0., 11., 8., 0.},
{ 0., 4., 12., 0., 0., 8., 8., 0.},
{ 0., 5., 8., 0., 0., 9., 8., 0.},
{ 0., 4., 11., 0., 1., 12., 7., 0.},
{ 0., 2., 14., 5., 10., 12., 0., 0.},
{ 0., 0., 6., 13., 10., 0., 0., 0.}}
Ms=SVD(A)
#3つの行列まとめて返すから、1,2,3番と番号をつけて表示してみる。
U=Ms(1)
S=Ms(2)
V=Ms(3)
# geogebraはベクトルと行列を区別している。行ベクトルは{}を2重にしないと行列と見ない。
# Sequence(Element(U(1),k),k,1,8) でUの1行ベクトルを8行1列行列に変換する。
# {V(1)}でVの1行ベクトルを1行8列行列に変換する。
# s1U1V1tだけでも以下のように長くなる。
x1=S(1,1) Sequence(Element(U(1),k),k,1,8) * {V(1)}
x2=Sum(Sequence(S(j,j) Sequence({Element(U(j),k)},k,1,8) {V(j)},j,1,2))
x3=Sum(Sequence(S(j,j) Sequence({Element(U(j),k)},k,1,8) {V(j)},j,1,3))
x4=Sum(Sequence(S(j,j) Sequence({Element(U(j),k)},k,1,8) {V(j)},j,1,4))
x5=Sum(Sequence(S(j,j) Sequence({Element(U(j),k)},k,1,8) {V(j)},j,1,5))
x6=Sum(Sequence(S(j,j) Sequence({Element(U(j),k)},k,1,8) {V(j)},j,1,6))
#このように近似を続けると、
x6 ≒ x0となる。