Routhova věta
Routhova věta
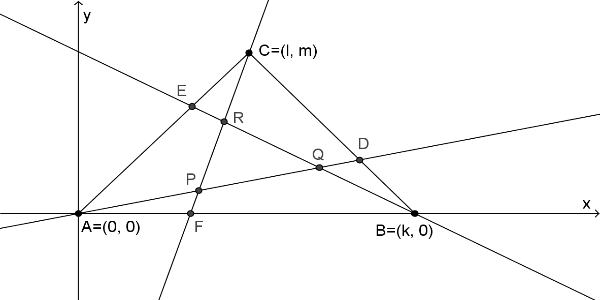
Necht' D, E, F jsou v uvedeném pořadí vnitřní body stran BC,CA a AB trojúhelníku ABC. Poměry jejich vzdáleností od krajních bodů příslušných stran nazvěme Dále označíme P, Q, R průsečíky dvojic úseček AD, BE a CF (tzv. ceviány) takto: . Potom poměr obsahů trojúhelníků PQR a ABC je dán výrazem:

Důkazy
Klasický důkaz a počítačový důkaz v programu CoCoa nalezneme v knize:
PECH, Pavel. Klasické vs. počítačové metody při řešení úloh v geometrii. 1. vyd. V Českých Budějovicích: Jihočeská univerzita, 2005, 170 s. ISBN 80-704-0805-7.
Důkaz využívající barycentrické souřadnice nalezneme v knize:
COXETER, H. Introduction to geometry. 2nd ed. New York: John Wiley & Sons, 1989, xvi, 469 s. Wiley classics library. ISBN 0471504580.
Důkaz využívající Menelaovu větu lze najít na stránce:
https://en.wikipedia.org/wiki/Routh%27s_theorem
Důkaz v CAS prostředí v GeoGebře:
Speciální případy Routhovy věty
Cevova věta
V trojúhelníku ABC se přímky AX, BY a CZ, kde bodyX, Y, Z leží na stranách protilehlých odpovídajícím vrcholům, protínají v jednom
bodě právě tehdy, když platí:
Tento případ nastane právě tehdy, když v Routhově větě platí xyz = 1, pak obsah trojúhelníku PQR je roven nule. Feynmanův trojúhelník Mějme libovolný trojúhelník v rovině. Jestliže každý jeho vrchol spojíme s bodem, který leží v jedné třetině protilehlé strany, pak trojúhelník tvořený těmito spojnicemi má obsah o velikosti jedné sedminy obsahu původního trojúhelníku. Jestliže body D, E, F dělí strany trojúhelníku ABC ve stejném poměru, pak x = y = z = f a po úpravě vzorce z Routhovy věty má tvar . Rozdělíme-li strany trojúhelníka na tři stejné díly, pak a z uvedeného vzorce plyne , že obsah trojúhelníku PQR je roven obsahu trojúhelníku ABC.