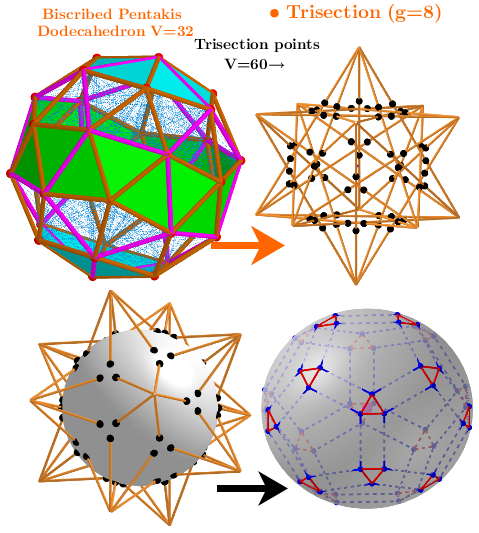
Rhombicosidodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 8th-order segments(Variant1)
A polyhedron is constructed whose V=60 vertices are the points of the trisection of the segments the same length 8th-order(g=8) of the Biscribed Pentakis Dodecahedron.
Geometric Constructions are in Applet: Series of polyhedra obtained by trisection (truncation) different segments of the original polyhedron, and the resulting polyhedra in Applet: Serie of polyhedra obtained by trisection (truncation) segments of the Biscribed Pentakis Dodecahedron.

1. Generating Elements of mesh modeling the surfaces of convex polyhedron and its dual image
2. Coloring edges and faces of polyhedra
3. Properties of polyhedra
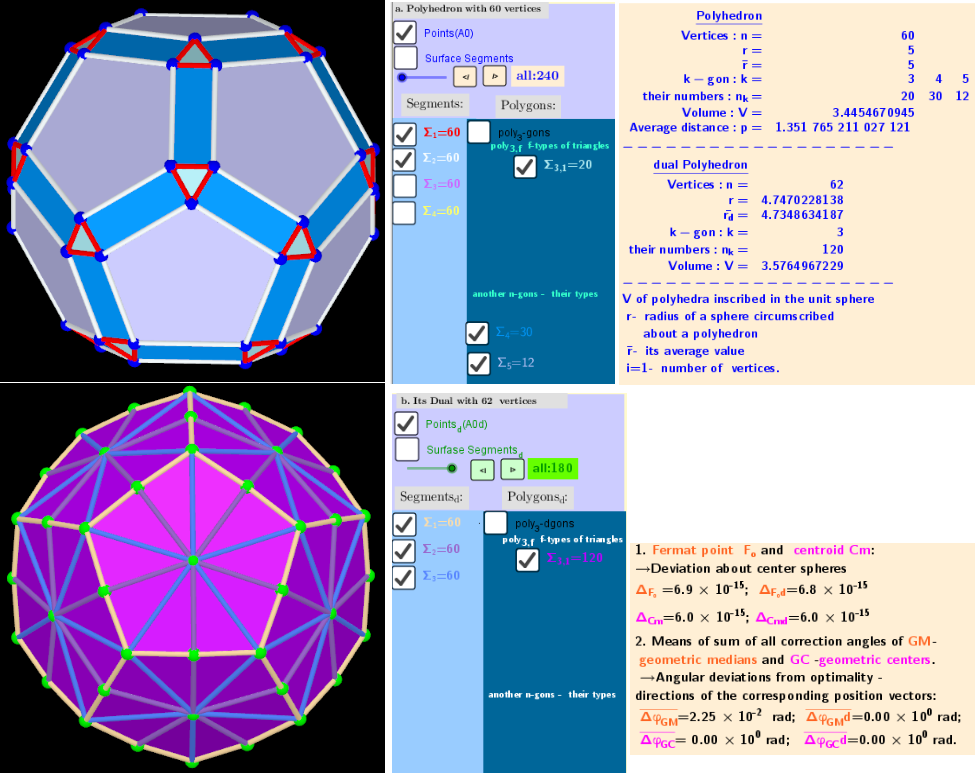
as Rhombicosidodecahedron
Dual
Vertices: 62 (30[4] + 20[6] + 12[10])
Faces: 120 (acute triangles)
Edges: 180 (60 short + 60 medium + 60 long)
| Vertices: | 60 (60[4]) |
| Faces: | 62 (20 equilateral triangles + 30 squares + 12 regular pentagons) |
| Edges: | 120 |
![[size=85][u]Comparing my images and from sources:[/u]
[b]Rhombicosidodecahedron-Deltoidal hexecontahedron[/b]
[url=https://en.wikipedia.org/wiki/Rhombicosidodecahedron]https://en.wikipedia.org/wiki/Rhombicosidodecahedron[/url]
[url=http://dmccooey.com/polyhedra/Rhombicosidodecahedron.html]http://dmccooey.com/polyhedra/Rhombicosidodecahedron.html[/url]
[url=https://en.wikipedia.org/wiki/Deltoidal_hexecontahedron]https://en.wikipedia.org/wiki/Deltoidal_hexecontahedron[/url];
[url=http://dmccooey.com/polyhedra/DeltoidalHexecontahedron.html]http://dmccooey.com/polyhedra/DeltoidalHexecontahedron.html[/url][/size]](https://www.geogebra.org/resource/eaysrrec/ySxLqwX8ZVHUrwoH/material-eaysrrec.png)