Renaissance
Vitruvius
De Architectura, het monumentale werk van de Romeinse architect Vitruvius uit 27 voor Christus, vormde de inspiratie voor Renaissancearchitecten als Alberti, Bramante, Michelangelo en Palladio.
Alberti (1407-1472) zag schoonheid als “Een rationele ordening en samensmelting van de proporties van alle delen van een gebouw, zodanig dat elk deel zijn absoluut vaststaande vorm en omvang heeft en niets kan worden toegevoegd of verwijderd zonder dat de harmonie van het geheel wordt verstoord”.
Hij schreef ook "We zullen daarom al onze regels voor verhouding ontlenen aan de muzikanten, die de grootste meesters zijn in de getallen en verhoudingen waarin de natuur zichzelf op zijn meest excellente en complete manier toont."
Dit sluit aan bij Ann Bulckens die via de middelevenredigheid 9 : 6 :: 6 : 4 de verhouding 3 : 2 zag als de sleutelverhouding in het Parthenon.
Palladio
In zijn "I quattro libri dell'architettura" (De vier boeken van de architectuur - 1570) suggereert Palladio 7 harmonieuze verhoudingen. Op de diagonaal van het vierkant () na, vind je deze verhoudingen terug in de toonladder van Pythagoras.
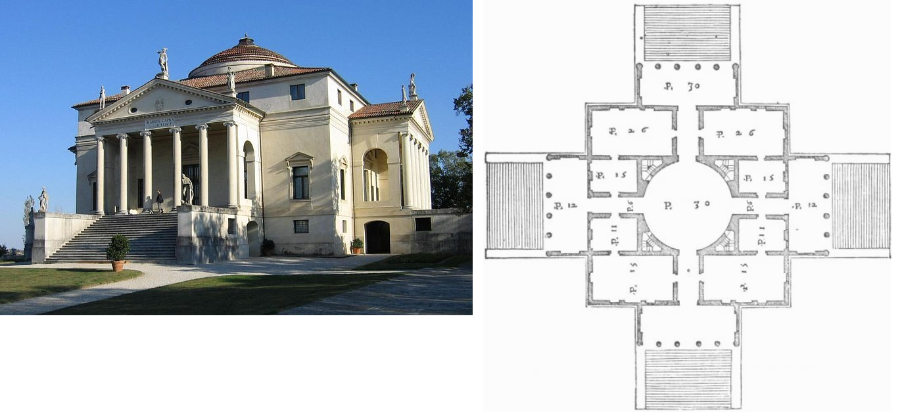
Een iconisch voorbeeld van renaissance architectuur is de Villa Rotonda (1570)van Palladio.
Grondplan en opstand van deze villa in Vicenza zijn opgebouwd vanuit cirkel en vierkant.
Bramante
Een ander iconisch gebouw uit de renaissance is het Tempietto (1510) van Bramante.
Bramante baseerde zich op Romeinse tempels en op Vitruvius, zij het niet 100%.
Dus ook in dit tempietto vind je klassieke verhoudingen.
De zuilen zouden even hoog moeten zijn als de cella breed, en de afstand tussen de rand van de stylobaat en de muur van de cella zou een vijfde moeten zijn van de diameter van de stylobaat, maar hier heeft Bramante zich niet aan gehouden. Daarentegen zijn andere verhoudingen wel volmaakt, zoals gebruikelijk bij renaissancegebouwen. Zo is de breedte van het peristylium of de zuilenrij (negen meter) gelijk aan de hoogte van de middelste cilinder (de cella en de tamboer). De afstand tussen de zuilen, als je die vanaf het middelpunt van de zuilen meet, is vier keer zo groot als de diameter van elke zuil, en de afstand tot de muur bedraagt twee keer de diameter (bron: Wikipedia).
Uiteraard kan je hier zoveel horizontale lijnen trekken, dat het niet moeilijk is om ergens een gulden rechthoek te vinden, al gaat dit volledig voorbij aan de opvattingen en de geschriften van renaissance architecten.

