Sucesión convergente
Una sucesión a(n) es convergente cuando tiene límite finito. El límite L de una sucesión a(n) es el número al que la sucesión se aproxima cada vez más. Se dice que la sucesión a(n) converge a su límite L y se expresa por
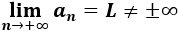 O bien, por a(n)→L.
Ejemplo 1: La sucesión a(n)=1/n es convergente a 0. Sus primeros términos son
O bien, por a(n)→L.
Ejemplo 1: La sucesión a(n)=1/n es convergente a 0. Sus primeros términos son
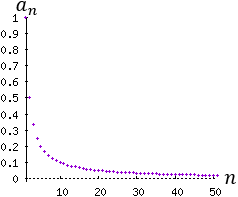
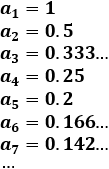 Cada término de la sucesión es menor que el anterior y cada vez se aproxima más a 0. El límite de la sucesión es L=0. Representación de la sucesión (n≤50):
Cada término de la sucesión es menor que el anterior y cada vez se aproxima más a 0. El límite de la sucesión es L=0. Representación de la sucesión (n≤50):
 Importante: El límite de una sucesión es único. Es decir, si una sucesión converge, converge a un único punto.
Si no existe el límite de la sucesión a(n) ó es infinito, se dice que la sucesión no converge. Nosotros diremos que la sucesión es divergente, aunque algunos reservan este nombre únicamente para las sucesiones que tienden a infinito.
Ejemplo 2: La sucesión a(n)=n^2 es divergente. Sus primeros términos son
Importante: El límite de una sucesión es único. Es decir, si una sucesión converge, converge a un único punto.
Si no existe el límite de la sucesión a(n) ó es infinito, se dice que la sucesión no converge. Nosotros diremos que la sucesión es divergente, aunque algunos reservan este nombre únicamente para las sucesiones que tienden a infinito.
Ejemplo 2: La sucesión a(n)=n^2 es divergente. Sus primeros términos son
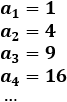 Representación de la sucesión (n≤50):
Representación de la sucesión (n≤50):
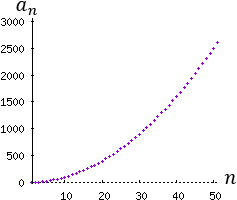 Se observa que la sucesión crece indefinidamente y no tiende a ningún valor finito.
Se observa que la sucesión crece indefinidamente y no tiende a ningún valor finito.
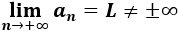 O bien, por a(n)→L.
Ejemplo 1: La sucesión a(n)=1/n es convergente a 0. Sus primeros términos son
O bien, por a(n)→L.
Ejemplo 1: La sucesión a(n)=1/n es convergente a 0. Sus primeros términos son
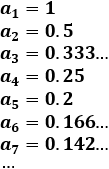 Cada término de la sucesión es menor que el anterior y cada vez se aproxima más a 0. El límite de la sucesión es L=0. Representación de la sucesión (n≤50):
Cada término de la sucesión es menor que el anterior y cada vez se aproxima más a 0. El límite de la sucesión es L=0. Representación de la sucesión (n≤50):
 Importante: El límite de una sucesión es único. Es decir, si una sucesión converge, converge a un único punto.
Si no existe el límite de la sucesión a(n) ó es infinito, se dice que la sucesión no converge. Nosotros diremos que la sucesión es divergente, aunque algunos reservan este nombre únicamente para las sucesiones que tienden a infinito.
Ejemplo 2: La sucesión a(n)=n^2 es divergente. Sus primeros términos son
Importante: El límite de una sucesión es único. Es decir, si una sucesión converge, converge a un único punto.
Si no existe el límite de la sucesión a(n) ó es infinito, se dice que la sucesión no converge. Nosotros diremos que la sucesión es divergente, aunque algunos reservan este nombre únicamente para las sucesiones que tienden a infinito.
Ejemplo 2: La sucesión a(n)=n^2 es divergente. Sus primeros términos son
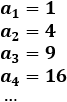 Representación de la sucesión (n≤50):
Representación de la sucesión (n≤50):
 Se observa que la sucesión crece indefinidamente y no tiende a ningún valor finito.
Se observa que la sucesión crece indefinidamente y no tiende a ningún valor finito.Problemas propuestos
Problema 1: A partir de las representaciones, determinar si las sucesiones son convergentes o no:
Sucesión 1:
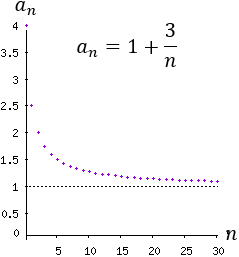 Sucesión 2:
Sucesión 2:
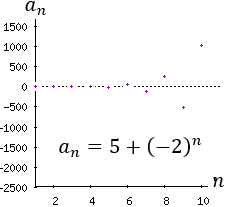 Sucesión 3:
Sucesión 3:
 Sucesión 4:
Sucesión 4:
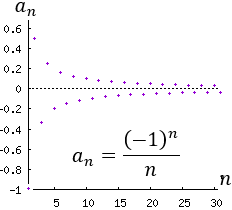 Problema 2: ¿Una sucesión constante puede ser divergente?
Problema 3: Una sucesión convergente se aproxima a su límite, ¿puede alcanzarlo?
Problema 4: Sea la sucesión
Problema 2: ¿Una sucesión constante puede ser divergente?
Problema 3: Una sucesión convergente se aproxima a su límite, ¿puede alcanzarlo?
Problema 4: Sea la sucesión
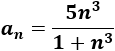 Calcular los 5 primeros términos para deducir cuál es su límite L y calcular la distancia entre dichos términos y L.
Problema 5: ¿Una sucesión alternada puede tener límite?
Enlace a las soluciones de los problemas: Tipos de sucesiones: convergencia, monotonía, sucesiones alternadas, sucesiones oscilantes y sucesiones acotadas.
Recursos de sucesiones:
Calcular los 5 primeros términos para deducir cuál es su límite L y calcular la distancia entre dichos términos y L.
Problema 5: ¿Una sucesión alternada puede tener límite?
Enlace a las soluciones de los problemas: Tipos de sucesiones: convergencia, monotonía, sucesiones alternadas, sucesiones oscilantes y sucesiones acotadas.
Recursos de sucesiones:
 Sucesión 2:
Sucesión 2:
 Sucesión 3:
Sucesión 3:
 Sucesión 4:
Sucesión 4:
 Problema 2: ¿Una sucesión constante puede ser divergente?
Problema 3: Una sucesión convergente se aproxima a su límite, ¿puede alcanzarlo?
Problema 4: Sea la sucesión
Problema 2: ¿Una sucesión constante puede ser divergente?
Problema 3: Una sucesión convergente se aproxima a su límite, ¿puede alcanzarlo?
Problema 4: Sea la sucesión
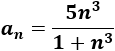 Calcular los 5 primeros términos para deducir cuál es su límite L y calcular la distancia entre dichos términos y L.
Problema 5: ¿Una sucesión alternada puede tener límite?
Enlace a las soluciones de los problemas: Tipos de sucesiones: convergencia, monotonía, sucesiones alternadas, sucesiones oscilantes y sucesiones acotadas.
Recursos de sucesiones:
Calcular los 5 primeros términos para deducir cuál es su límite L y calcular la distancia entre dichos términos y L.
Problema 5: ¿Una sucesión alternada puede tener límite?
Enlace a las soluciones de los problemas: Tipos de sucesiones: convergencia, monotonía, sucesiones alternadas, sucesiones oscilantes y sucesiones acotadas.
Recursos de sucesiones:
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente