4.2 Como Calcular a distância no espaço
Introdução
Aqui, será apresentado como calcular a distância entre duas retas no espaço, que será denotada como D(f,g). Vale lembrar que quando se fala de distância entre duas retas, quer-se referir à menor distância entre elas. Para ajudar um pouco na visualização dos exercícios é necessário a apresentação da reta reversa, que são retas que não pertencem ao mesmo plano, como exemplo da figura abaixo:
Arraste a figura para a visualização ficar mais clara.
Não se pode adotar a estratégia feita ,por exemplo, no cálculo da distância de duas retas no mesmo plano: de escolher um ponto qualquer de uma das retas e fazer a distância desse ponto até à outra reta. Porque nesse caso as distâncias entra as duas retas não são sempre constantes, ou seja , elas não são paralelas
Teoria
Para a demonstração de como se chega ao cálculo da distância é bom dar destaque à alguns elementos importantes:
-Vetor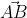 
, é o vetor que liga um ponto A qualquer da reta f à um ponto B qualquer da reta g. Aqui, é importante lembrar que é você quem escolhe os pontos B e A, a única condição que precisa atender é a de que tem que pertencer às respectivas retas.
-Vetor 
, é o vetor diretor da reta f.
-Vetor 
, é o vetor diretor da reta g.
A estratégia para calcular a menor distância entre essas retas é parecida de como foi feito anteriormente para calcular a distância entre ponto e reta. Porém ao invés de analisar um paralelogramo, é mais vantajoso analisar o paralelepípedo.
Como o que está sendo analisado é um paralelepípedo, é muito importante enxergar ele. É importante lembrar que o paralelepípedo é interessante de ser usado porque é possível trabalhar nele usando produto misto.
Aqui estão os três vetores importantes para o cálculo da distância, eles foram deslocados para ser possível ver o paralelepípedo formado por eles:
E aqui o paralelepípedo formado por eles:
Vetor diretor de f=
Vetor diretor de g=
Vetor que liga um ponto qualquer de f à um ponto qualquer de g=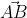
Volume=Área base * Altura
Volume=Produto misto= 
Os dois volumes são equivalentes, logo, podemos relaciona-los.
Como está bem evidente, a Área base = 
, que é o módulo do produto vetorial entre os vetores e .
Produto misto=Área base * Altura
E assim, a fórmula final da distância entre duas retas fica:
Sabe-se que o volume do paralelepípedo é: Volume=Área base X Altura
Essa altura é o que interessa, pois ela será a distância desejada entre as duas retas.
A área da base(em vermelho) e a altura vistas de forma mais clara:
Arrastando o controle deslizante t, perceba que só tem uma distância que será mínima