4. El ciclo de quintas
Esta actividad pertenece al libro de GeoGebra Música y Matemáticas.
Teclas blancas: incongruencias módulo 7
Volvamos al piano, con sus 52 teclas blancas (del total de 88 teclas):

Observamos que cada octava, entre la 1 y la 7, comprende siete teclas blancas que, de izquierda a derecha, corresponden a las notas Do, Re, Mi, Fa, Sol, La y Si.
Podemos comprobar la gran similitud entre las definiciones de octava y nota con las ya mencionadas de semana y día de semana:
semana 1 = {L1, M1, X1, J1, V1, S1, D1}
octava 1 = {Do1, Re1, Mi1, Fa1, Sol1, La1, Si1}
[viernes] = {V0, V1, V2, V3, V4, V5...} = {5, 12, 19, 26, 33, 40...}
[La] = {La0, La1, La2, La3, La4, La5...} = {27.5, 55, 110, 220, 440, 880...}
¿Estamos entonces ante la misma situación que los siete días de la semana, correspondiendo Do al lunes y Si al domingo? No exactamente, por desgracia.
La diferencia fundamental reside en que la distancia de un lunes al día siguiente, martes (más precisamente, la distancia entre el comienzo de ambos días), es de un día, la misma que hay entre un miércoles y su consecutivo jueves. Sin embargo, la “distancia sonora” (razón entre frecuencias) entre el Do y el Re es mayor que entre el Mi y el Fa.
Pero, ¡esto es un gran problema! Si las distancias no son iguales, los cálculos con aritmética modular se vienen abajo, pues solo son practicables con notas del mismo nombre (separadas un número entero de octavas). Así que... ¡es preciso modular la escala!
El ciclo de quintas
El origen de este problema se remonta al nacimiento de esas notas, cuyos intervalos o distancias fueron establecidas por los pitagóricos. En esencia, los pitagóricos aplicaron sistemáticamente dos intervalos fijos, la octava y la quinta, para obtener los demás, aparte de la cuarta (ver el artículo de Vicente Liem ya mencionado). Los intervalos resultantes resultaron simples, pero desiguales, dando lugar a la popular escala diatónica: Do, Re, Mi...
La quinta es el intervalo que separa la altura de sonidos cuyas frecuencias están en proporción 3:2.
Así, partiendo del La4, y subiendo cada vez una quinta, se obtienen las siguientes frecuencias:

Ejemplificaremos ahora el método seguido por los pitagóricos para construir la escala diatónica. Los pitagóricos se dieron cuenta que había cierta relación entre la longitud de una cuerda y el sonido que producía. Hoy sabemos que esa relación se basa en que la frecuencia es inversamente proporcional a la longitud.
Empezamos con una frecuencia determinada (correspondiente a la frecuencia fundamental de vibración de una cuerda de longitud dada). Supondremos, para mayor claridad, que esa frecuencia F es justamente la del Do central del piano: Do4. Sigamos los siguientes pasos:
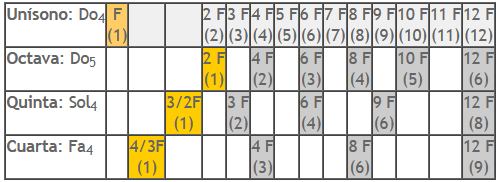
- Do4 = F (unísono).
- Dividiendo la cuerda en dos partes iguales (no hace falta cortarla, basta sujetarla), se obtiene una cuerda la mitad de larga que, al ser pulsada, emite una frecuencia fundamental exactamente el doble que la anterior: Do5 = 2 F. Ya tenemos el intervalo de octava (en griego, diapasón), que es el intervalo que queremos dividir en intervalos menores.
- Dividiendo la cuerda original en tres partes iguales, la cuerda de longitud 2/3 emite una frecuencia fundamental exactamente 3/2 de veces la original: Sol4 = 3/2 F. Este es el intervalo de quinta (en griego, diapente).
- Dividiendo la cuerda original en cuatro partes iguales, la cuerda de longitud 3/4 emite una frecuencia fundamental exactamente 4/3 de veces la original: Fa4 = 4/3 F. Este es el intervalo de cuarta (en griego, diatesaron).
Ahora proseguimos con el método conocido como ciclo de quintas:
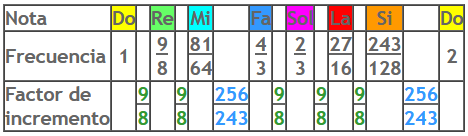
- Subiendo una quinta a partir de la quinta, es decir, tomando 4/9 de la longitud de la cuerda obtenemos la nota Re5 = 9/4 F. Como hemos sobrepasado la octava, nos quedamos con el doble de esa longitud, y por tanto la mitad de frecuencia: Re4 = 9/8 F. Este es el intervalo de segunda.
- Subiendo de nuevo una quinta, es decir, tomando 2/3 de 8/9 de la longitud original, obtenemos una nueva longitud de cuerda cuya frecuencia corresponde a La4 = 27/16 F. Este es el intervalo de sexta.
- Subiendo otra quinta a partir de la anterior obtenemos Mi5 = 81/32 F. Como nos volvemos a pasar de octava, duplicamos la cuerda para obtener la mitad de frecuencia: Mi4 = 81/64 F. Este es el intervalo de tercera.
- Por último, subiendo otra quinta más a partir de la anterior obtenemos Si4 = 243/128 F. Este es el intervalo de séptima.