Површина равног лика
ПРИМЕНА ОДРЕЂЕНОГ ИНТЕГРАЛА У ИЗРАЧУНАВАЊУ ПОВРШИНЕ
Нека је функција у=f(x) дефинисана, непрекидна и f(x) 0 на [a,b]. Тада је површина криволинијскг трапеза ограниченог одсечком [a,b] на х оси , графиком функције и ординатама x=a и x=b једнака
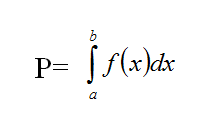
Односно, у општем случају
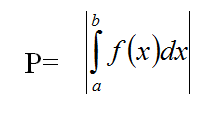
Пример
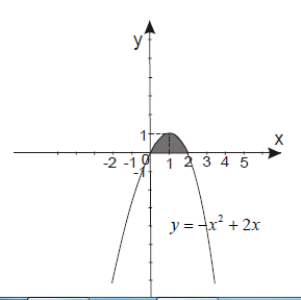
Израчунати површину фигуре ограничену луком криве y=-x2 +2x и x-осом.