Parabola je svuda oko nas
Matematičari često kažu da je matematika svuda oko nas, da je tako govore i sljedeći primjeri. Mnogi sportovi uključuju predmete koji se bacaju, šutiraju ili udaraju, a zatim nastavljaju bez dodatnih sila. Takvi se predmeti nazivaju projektili. Putanje projektila, kao i njihove visine tokom vremena, mogu da se modeliraju kvadratnim funkcijama.
Koju putanju opisuje lopta ili kugla koju uputi neki od sportista?

Koju putanju opisuju kapi vode u vodoskocima? Koja je maksimalna visina?

Ogovor je jedan: PARABOLU.
Sve navedene putanje kao i mnoge druge primjeri su kosog hica. Kosi hitac predstavlja kretanje tijela pod određenim uglom. Kosi hitac uvijek ima početnu brzinu i ugao pod kojim je tijelo bačeno. Ono se takođe kreće i staje u tački čija normala (na Zemlju) predstavlja maksimalnu visinu tog hica. Tijelo pada na isti način kao što se i pelo do maksimalne visine. Takva linija naziva se parabola. Parabola je svuda u našem okruženju. Mostovi se često grade tako da im lukovi imaju oblik parabole.

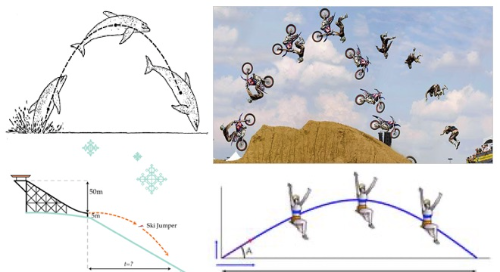
Parabolu imama kod skijaških skokova, egzibicija motociklista, ipsaljivanje topovskih zrna, skokova u vodi....
Funkciju nazivamo kvadratnom, ako su , i realni brojevi i . Grafik kvadratne funkcije je parabola. Tačka u kojoj kvadratna funkcija dostiže najmanju (najveću) vrijednost nazivamo tjeme parabole.
Ispitivanje svojstava kvadratne funkcije započinjemo razmatranjem specijalnog sluučaja . Za dobijamo funkciju .
![Grafik kvadratne funkcije [math]y=ax^2[/math], za [math]a=1[/math]](https://www.geogebra.org/resource/m6rjjzvs/fdMeYxWLm0v80PKr/material-m6rjjzvs.png)
Pomjeranjem klizača pogledajte kako izgleda grafik kvadratne funkcije .
Kao što vidimo za tjeme je tačka minimuma, a za je tačka maksimuma.