Przykład 4.6
Obliczymy i porównamy objętości dwóch brył powstałych przez obrót krzywej dla najpierw dokoła osi , a następnie dokoła osi .
Rozwiązanie: Poniższy aplet ilustruje jak powstają powierzchnie ograniczające rozważane bryły. Zmieniając kąt obrotu dla krzywej określonej na przedziale oraz pionowego odcinka łączącego prawy koniec krzywej z jego prostokątnym rzutem na oś otrzymamy domkniętą powierzchnię obrotową wokół osi . Postępując podobnie względem osi otrzymamy drugą.
Wskazówka: Rozwiń listy Powierzchnia , Odcinek oraz Krzywa parametryczna, aby pokazać lub ukryć obiekty. Dla powierzchni utwórz "górną pokrywkę" wzorując się na określeniu powierzchni .
Oznaczmy wykreślone bryły odpowiednio przez oraz . Ich objętości możemy wyrazić za pomocą całek:
Skorzystamy teraz z Widoku CAS, aby obliczyć i porównać wartości tych całek.
Uwaga 1. Rozważaną w zadaniu krzywą możemy zapisać jako: dla .
Uwaga 2. W GeoGebrze funkcje cyklometryczne są zapisywane w formie np. funkcje zamienią się automatycznie na .
Uwaga 3. Aby otrzymać wartości przybliżone oraz wystarczy w pasku narzędzi (Widoku CAS) przestawić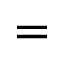 
na 
. Można też wprowadzić np. i otrzymać wartość logiczną zdania .
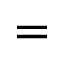na . Można też wprowadzić np. i otrzymać wartość logiczną zdania .Która z brył ma większą objętość?