Dimensi Tiga
Dimensi tiga merupakan bangun ruang yang terbentuk dari 3 elemen yaitu titik, garis, dan bidang. Titik adalah lukisan tanda noktah yang dibubuhi nama menggunakan huruf kapital. Suatu titik tidak memiliki besaran dan tidak berdimensi. Garis adalah himpunan titik-titik yang hanya memiliki ukuran panjang dan berdimensi satu. Sedangkan bidang adalah himpunan titik-titik yang memiliki ukuran panjang dan luas, sehingga dikatakan berdimensi dua.
Adapun materi yang akan kita pelajari dalam dimensi tiga ini adalah
Jarak titik ke titik
Jarak titik ke garis
Jarak titik ke bidang
Jarak Titik ke Titik
Ilustrasi di bawah ini memeragakan jarak antara titik A dan titik B.
Jarak antara titik A dan titik B sama dengan panjang ruas garis AB.
Geserlah titik A atau B untuk melakukan peragaan
Lalu bagaimana cara menentukan jarak antar titik dalam ruang? masih ingatkah kalian dengan teorema pythagoras?
Ya, teorema pythagoras digunakan untuk menentukan panjang sisi salah satu segitiga siku-siku.


Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Titik I merupakan titik tengah rusuk DH. Tentukan jarak antara titik I dengan titik F.
Langkah Penyelesaian
1. Gambarlah kubus ABCD.EFGH
2. Hubungkan titik I dan titik F dengan sebuah garis.
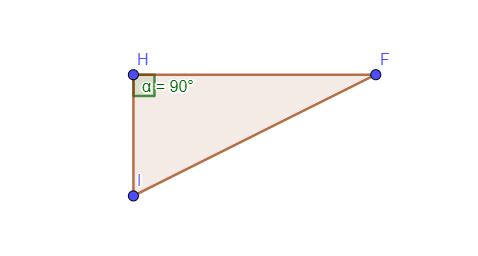
3. Buatlah segitiga siku-siku yang melalui titik I, F, dan satu titik lain (misal segitiga IFH)
4. Hitunglah panjang ruas garis IF menggunakan teorema Pythagoras.
Jarak antara titik I dan titik F.
Pembahasan
Jarak Titik ke Garis
Jarak titik ke garis adalah ruas garis yang tegak lurus atau terpendek dari sebuah titik terhadap sebuah garis. Misal A adalah titik dan g adalah garis. Jarak titik A ke garis g adalah panjang ruas garis AB dengan B terletak di garis g, dan AB tegak lurus dengan garis g.

Prosedur Menghitung Jarak Titik ke Garis
Adapun langkah-langkah untuk menghitung jarak titik A ke garis g dengan bantuan titik B, C, dan D sebagai berikut.

- Menghubungkan titik A ke titik C dan titik D sehingga terbentuk segitiga ACD seperti gambar di bawah.

- Kemudian, menghitung jarak antar dua titik, yaitu AC, AD, dan CD untuk menetapkan jenis segitiga.
- Terakhir yakni, menghitung tinggi segitiga ACD, yaitu AB yang merupakan jarak titik A ke garis g.
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jarak titik A ke rusuk HG adalah….
Langkah penyelesaian
- Gambarlah kubus ABCD.EFGH
- Hubungkan titik A dengan titik G dan H sehingga membentuk segitiga AGH.
- Tetapkan jenis segitiga yang terbentuk
Jarak titik A ke rusuk HG
Pembahasan
Perhatikan segitiga AHG siku-siku di H.
 Jarak titik A ke rusuk HG adalah panjang ruas garis AH, ()
, (AH diagonal sisi)
Jadi jarak A ke HG = cm
Jarak titik A ke rusuk HG adalah panjang ruas garis AH, ()
, (AH diagonal sisi)
Jadi jarak A ke HG = cm
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jarak titik B ke diagonal AG adalah….
Langkah penyelesaian
- Gambarlah kubus ABCD.EFGH
- Hubungkan titik B dengan titik A dan G sehingga membentuk segitiga ABG
- Tetapkan jenis segitiga yang terbentuk
Lihat segitiga ABG
, BG diagonal sisi
, AG diagonal ruang
Pembahasan
Perhatikan segitiga siku-siku ABG
Jadi jarak titik B ke AG adalah .
Contoh
Diketahui T.ABCD limas beraturan. Panjang rusuk alas 12 cm, dan panjang rusuk tegak cm. Jarak A ke CT adalah . . .
Langkah penyelesaian
1. Gambarlah limas T.ABCD
1. Hubungkan titik A dengan titik C dan T sehingga membentuk segitiga ACT
2. Tetapkan segitiga yang terbentuk
Perhatikan segitiga sama sisi ACT
Pembahasan
Perhatikan ACP
Jadi, jarak titik A ke CT adalah cm.
Jarak Titik ke Bidang
Garis tegak lurus Bidang
 Garis tegak lurus sebuah bidang jika garis tersebut tegak lurus dua buah garis berpotongan yang terdapat pada bidang.
Garis tegak lurus sebuah bidang jika garis tersebut tegak lurus dua buah garis berpotongan yang terdapat pada bidang.
Jarak titik ke bidang
Jarak antara titik A ke bidang V adalah panjang ruas garis yang menghubungkan tegak lurus titik A ke bidang .
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jarak titik F ke bidang ABCD adalah . . .
Langkah penyelesaian
1. Gambarlah kubus ABCD.EFGH
2. Proyeksikan titik F tegak lurus terhadap bidang ABCD
Jarak titik F ke bidang ABCD
Pembahasan
Titik F diproyeksikan tegak lurus ke bidang ABCD, sehingga FB tegak lurus terhadap bidang ABCD.
Jarak titik F ke bidang ABCD = panjang rusuk FB = 6 cm
Jadi, jarak titik F ke bidang ABCD adalah 6 cm.
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 10 cm. Jarak titik A ke bidang BDHF adalah . . .
Langkah penyelesaian
1. Buatlah kubus ABCD.EFGH
2. Proyeksikan titik A tegak lurus terhadap bidang BDHF
Pembahasan
Titik A diproyeksikan tegak lurus terhadap bidang BDHF, sehingga AP tegak lurus terhadap bidang BDHF.
Jarak titik A ke bidang BDHF = panjang ruas garis AP ()
, AC diagonal sisi
Jadi jarak titik A ke bidang BDHF adalah cm.
Contoh
Diketahui kubus ABCD.EFGH dengan panjang rusuk 9 cm. Jarak titik C ke bidang BDG adalah . . .
Perhatikan ilustrasi berikut untuk menjawab pertanyaan di atas!
Lalu berapakah jarak titik E ke bidang BDG?
Dapatkah kalian mengambil kesimpulan?
KESIMPULAN
Pada kubus ABCD.EFGH dengan panjang rusuk satuan. Berlaku bahwa
1. Jarak titik C ke bidang BDG adalah satuan.
2. Jarak titik E ke bidang BDG adalah satuan.