Fläche zwischen zwei Graphen
Fast alle Flächen
Bisher konnten wir nur Flächen und Flächenbilanzen zwischen einem Funktionsgraphen und der Abszisse berechnen. Aber das hilft nur bei solchen Flächen, die auf einer Seite - bei der Abszisse - eine gerade Begrenzung haben.
Wenn es möglich ist, die Fläche zwischen zwei Funktionsgraphen zu berechnen, dann kann man schon fast alle beliebigen Flächen damit berechnen:
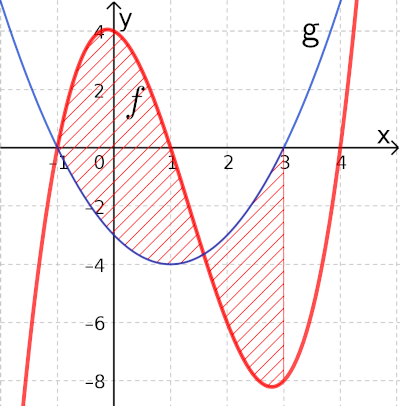
Zurückführen auf ein bekanntes Problem
Im Bild oben sind die Funktionsgraphen der Funktion und der Funktion dargestellt. Außerdem ist die Fläche zwischen den Funktionsgraphen im Intervall markiert.
Bei Flächen, die zwischen zwei Graphen liegen, gilt nicht mehr, dass alle Flächen unter der Abszisse negativ und die über der Abszisse positiv sind!
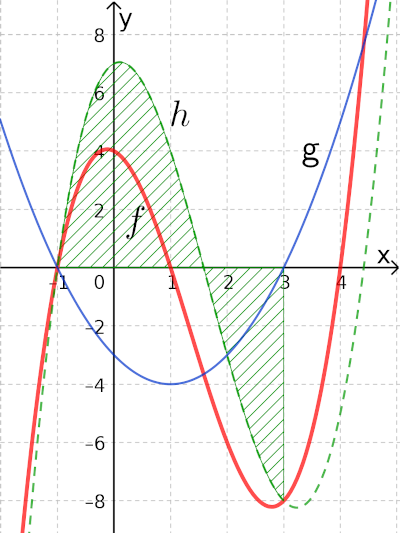
Für das Berechnen von Flächen und Flächenbilanzen zwischen zwei Funktionsgraphen bilden wir zuerst eine Differenzfunktion: .
- Die Flächenbilanz zwischen den Funktionsgraphen von und ist genau die Flächenbilanz, die die Differenzfunktion mit der Abszisse einschließt.
- Die Fläche zwischen den Funktionsgraphen von und ist genau die Fläche, die die Differenzfunktion mit der Abszisse einschließt.
Übungen zur Flächenberechnung
Im folgenden Applet kann man sich zum Einen jeweils die Differenzfunktion ansehen und zum Anderen kann es genutzt werden, um das Berechnen von Flächen zwischen zwei Grafen zu üben: