Which Integration Method?
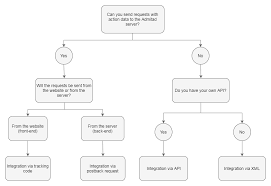
Integration is the process of finding the antiderivative of a function. There are several integration methods, each suited for different types of functions. Here are some common integration methods along with situations where they are approximate for specific functions:
1. Direct Integration (Basic Rules):
Method: Direct integration involves using basic integration rules to find the antiderivative of a function. Common rules include the power rule, constant rule, sum/difference rule, and trigonometric integrals.
Approximate Situation: Direct integration is suitable for elementary functions, such as polynomials, trigonometric functions, exponential functions, and their combinations.
Example: , where (C) is the constant of integration.
2. Integration by Parts:
Method: Integration by parts is a technique that transforms a product of functions into a different, hopefully more easily integrable form. The formula is given by: where (u) and (v) are chosen functions.
Approximate Situation: Integration by parts is useful when dealing with products of functions and can be used repeatedly in some cases.
Example: . Let u = x and dv = sin(x) dx, then du = dx and v = -cos(x). Applying the integration by parts formula, we get:
3. Trigonometric Substitution:
Method: Trigonometric substitution involves making a substitution based on a trigonometric identity to simplify an integral, typically in the case of radical expressions involving trigonometric functions.
Approximate Situation: Trigonometric substitution is useful for integrals involving square roots and trigonometric functions.
Example: . Using the substitution , we get:
Substituting back , we get
.
4. Partial Fraction Decomposition:
Method: Partial fraction decomposition is used to break down a rational function into simpler fractions for easier integration.
Approximate Situation: Partial fraction decomposition is useful for integrating rational functions.
Example: . Using partial fraction decomposition, we write
. Solving for A and B, we get:
These are just a few of the many integration methods available. The choice of method depends on the complexity of the integrand and the nature of the function being integrated. In practice, integration often requires creativity and a combination of techniques to arrive at a solution.