11。加法定理の活用
Rの座標に着目しよう。
0。加法定理の証明に向けて
<三角比の和差による>
上の画像で図形を確認しよう。
・和の正弦公式を作る
点OにA、Bがあつまるように直角三角形を3つかく。
△OPQは角O=Aで、Pが直角。△OQRは角O=Bで、角Qが直角。△ORSは角O=A+Bで、角Sが直角。
点Qから辺RSにおろした垂線の足をTとすると、TSPQが長方形になり、
Aをもつ△OPQと相似な三角形が他に3つできる。特に△QRTを利用する。
AとBが鋭角で、和が90未満の場合は上の図によって証明できる。
sin(A+B)=RS/OR=
・のこりの公式
和の正弦、差の正弦、和の余弦、差の余弦の4つは、1つがわかると他も出せる。
sin(A−B)=sin(A+(-B))=sinAcos(-B)+cosAsin(-B)=
cos(A+B)=OS/OR=
または、cos(A+B)=sin(90°-(A+B))=sin((90°-A)+(-B))
=
cos(A-B)=cos(A+(-B))=cosAcos(-B)-sinAsin(-B)=
<単位円で余弦定理>
自分で図をかいて、自分で計算して確認しよう。
・差の余弦公式を作る
2点P(cosA,sinA),Q(cosB,sinB)を単位円上にとる。角POQ=A-B>0でπ未満のとき、
△POQで余弦定理を使うと、
cos(A-B)=(OP²+OQ²ーPQ²)/(2・OP・OQ)
=
角POQがπをこえるとき、cosPOQ<0になり、2πーPOQはπをこえず、
cos(2πーPOQ)=cosPOQだから、上記と同様。
・のこりの公式は上と同じように出せるね。
<単位円×三角比の和差>
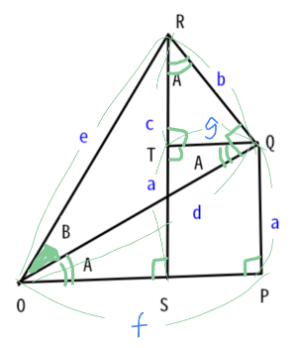
冒頭のアプレットで確認しよう。
単位円Oで、角POQ=B、角QOR=Aとする。
斜辺OR=1とすると、直角三角形ORQで、OQ=cosA,QR=sinA。
直角三角形OPQで、0P=cosAcosB,PQ=cosAsinB。
斜辺RQの直角三角形QRSを角RQC=Bとなるように、PSを直線にする。
CQ=sinAcosB,RS=sinAsinB。
すると、
sin(A+B)=点Rのy座標=sin(A+B)=SQ+QP=sinAcosB+cosAsinB
cos(A+B)=点Rのx座標=OP-RS=cosAcosB-sinAsinB
1.加法定理の特徴を観察する
簡単のためにsinAをsA,cosAをcA,tanAをtAとかくことにします。
<和の正弦・余弦・正接>
s(A+B)=sAcB+cAsB(スコ+コス)
c(A+B)=cAcB-sAsB(ココースス)
t(A+B)=(tA+tB)/(1-tAtB)(和/1-積)
<差の正弦・余弦・正接>(符号が和と逆になる。)
s(A-B)=sAc(-B)+cAs(-B)=sAcB-cAsB(スコーコス)
c(A-B)=cAc(-B)-sAs(-B)=cAcB+sAsB(ココ+スス)
t(A-B)=(tA+t(-B))/(1-tAt(-B))=(tA-tB)/(1+tAtB)=(差/1+積)
以下の積和公式、和積公式は上記の和と差の加法定理をペアにして
+ーが消し合う関係性として覚えていれば自然に導かれる。
<積→和>
s(A+B)+s(A-B)=2sAcBになる。だから、sAcB=1/2(s(A+B)+s(A-B))。
s(A+B)ーs(A-B)=2cAsBになる。だから、cAsB=1/2(s(A+B)ーs(A-B))。
c(A+B)+c(A-B)=2cAcBになる。だから、cAcB=1/2(c(A+B)+c(A-B))。
c(A+B) ーc(A-B)=-2sAsBになる。だから、sAsB=-1/2(s(A+B)ーs(A-B))。
<和→積>
A+B=P,A-B=Qとすると、A=(P+Q)/2, B=(P-Q)/2
s(A+B)+s(A-B)=2sAcBになる。だから、s(P)+s(Q)=2s(P+Q)/2 c(P-Q)/2。
s(A+B)ーs(A-B)=2cAsBになる。だから、s(P)ーs(Q)=2c(P+Q)/2 s(P-Q)/2。
c(A+B)+c(A-B)=2cAcBになる。だから、c(P)+c(Q)=2c(P+Q)/2 c(P-Q)/2。
c(A+B)ーc(A-B)=-2sAsBになる。だから、c(P)ーc(Q)=-2s(P+Q)/2 s(P-Q)/2。
(例)
sin15°==
sin15°==
cos15°==
sin75°=sin(90-15)°=cos15°=。cos75°=sin15°=
(例)y=1/5x+1とy=2x+1の作る角θのtanθは?
(例)「三角形ABCでsin2A+sin2B+sin2C=4sinAsinBsinCが成り立つ」の理由は?
A+B=180-Cなので、sin(A+B)=sinC, cosC=cos(180-(A+B))=-cos(A+B)の置き換えができる。
サインの和積と置き換えから、sin2A+sin2B=2sin(A+B)cos(A-B)=2sinCcos(A-B)
サインの加法と置き換えから、sin2C=2sinCcosC=2sinC(-cos(A+B))
左辺=2sinC(cos(A-B)-cos(A+B))=...(展開整理)...=2sinC・2sinAsinB=右辺
(例)「三角形ABCでsinA+sinB+sinC=4cosA/2cosB/2cosC/2が成り立つ」の理由は?
A+B=180-Cから(A+B)/2=90-C/2、sin((A+B)/2)=cos(C/2),sin(C/2)=cos((A+B)/2)の置き換えができる。
サインの和積と置き換えから、sinA+sinB=2sin((A+B)/2)cos((A-B)/2)=2cos(C/2)cos((A-B)/2)
サインの加法と置き換えから、sin2(C/2)=2sin(C/2)cos(C/2)=2cos((A+B)/2)cos(C/2)
左辺=2cos(C/2)(cos((A-B)/2)+cos((A+B)/2))=...(展開整理)...=2cosC/2・2cosA/2cosB/2=右辺
(例)「xが0と2πの間のとき、の解」は?
和積の公式「sin(P)ーsin(Q)=2cos sin」を使って、サインの差を積に直そう。
和がPで差Qとなる2数は和差算から、大=(P+Q)/2, 小=(P-Q)/2と出せるね。
和が9/2xで、差が1/2xの2数は大=5/2xと小=2x。
xが0と2πの間だからp=5/2xは0と5πの間。cosp=0よりp=1/2π(1,3,5,7,9)で、
x=2/5・p=1/5π(1,3,5,7,9)=1/5π, 3/5π, π, 7/5π, 9/5π
xが0と2πの間だからq=2xは0と4πの間。sinq=0よりq=π,2π,3πで、x=1/2π(1,2,3)
これより、x=1/2π, 3/2π。
まとめると、
(例)「cos(n+2)θ-2cosθcos(n+1)θ+cosnθ=0の理由とその利用例」は?
・理由
積和の公式「cosAcosB=1/2(cos(A+B)+cos(A-B))」から、2cos(n+1)θcosθ=cos(n+2)θ+cosnθ。
・利用例
cos(n+2)θ=2cosθ・cos(n+1)θ -cosnθを使って、最後にcosθ=cとおき、cの多項式にしてみよう。
n=-1:cos θ=2cosθ・cos0 -cos(-θ)=2c-c=c
n=0:cos2θ=2cosθ・cosθ -cos0 =2c2-1
n=1:cos3θ=2cosθ・cos2θ-cosθ =2c(2c2-1)-c=4c3-3c
n=2:cos4θ=2cosθ・cos3θ-cos2θ=2c(4c3-3c)-(2c2-1)=8c4-6c2-2c2+1=8c4--8c2+1
n=3:cos5θ=2cosθ・cos4θ-cos3θ=2c(8c4--8c2+1)-(4c3-3c)=16c5-16c3+2c -(4c3-3c) =16c5-20c3+5c
n=4:cos6θ=2cosθ・cos5θ-cos4θ=2c(16c5-20c3+5c)-(8c4--8c2+1)=32c6-40c4+10c2-(8c4--8c2+1)
=32c6-48c4+18c2-1
..................
こうして、漸化式として使えば、多倍角のコサインはコサインθの多項式になる。
cosmθの最高次数項=2m-1cmで、そのあとの次数は2ずつ小さくなっていくね。
2.倍角と半角の利用
簡単のためにsinAをsAやsと、cosAをcAやcと,tanAをtAとかくことにします。
<2倍角>
加法定理の和の公式で、2a=a+aとして導く。
s2A=s(A+A)=2sc。(これっきり)
c2A=c(A+A)=(c)²-(s)²=2c²-1=1-2s²。(1種の2乗は逆算できる)
t2A=
(例)「s+c=1/√2のときのc2Aの値」は?
辺々2乗して、1+2sc=1/2。2sc=1/2-1=-1/2=s2A。
(c2A)²=1-(s2A)²=1-(-1/2)²=3/4。c2A=+-√3/2
(例)「aがπ/2とπの間(cosaが負、sinaが正)でsina=3/5のときの、sin2a,co2s」は?
cosa=-4/5となるので、sin2a=2sinacosa=-12/25, cos2a=1-2・(3/5)2=7/25=2(-4/5)2-1
(例)「tanθ/2=t(t≠±1)として、sinθ、cosθ、tanθをtの式で表す」と?
θ/2=aとかくと、sinθ=sin(2a)=2sina・cosa=2t・cos2a=2t・1/(1+t2)=
cosθ=cos(2a)=2cos2a-1=2・1/(1+t2)-1=(2-(1+t2))/(1+t2)=
tanθ=sinθ/cosθ=
<半角>
s2(A/2)=(1−c)/2
c2(A/2)=(1+c)/2
t2(A/2)=(1-c)/(1+c)
(理由)a=2A、A=a/2で倍角cos公式を言い換えただけ。
(用途)サインコサインの2次式を1次式にしたいとき、微分・積分のときに役立つね。
(例)Aが鋭角でcosA=1/2のとき、cos2Aと、cos(A/2)の値は?
cos2A=2cos²A-1=2・(1/2)²-1=-1/2。
cos²(A/2)=(1+cosA)/2=(1+1/2)/2=3/4。cos(A/2)>0から、cos(A/2)=1/2√3。
(例)cos15°=x, sin15°=y の値は?
から、y=1/4x。
これから、x²=。
15°は鋭角だから、x=>0、y=。
(例)「aがπ/2とπの間(cosaが負、sinaが正)でsina=3/5のときの、sin(a/2),cos(a/2)」は?
cosa=-4/5となるので、sin2(a/2)=(1-cosa)/2=9/10 sin(a/2) = 3√10/10
cos2(a/2)=(1+cosa)/2=1/10 cos(a/2)=√10/10
3.多倍角の公式
<3倍角>
sin,cosをs,cと、sinA=s, cosA=cと略す。係数の符号が反転している。
s(3A)=。
c(3A)=。
(理由)加法定理、2倍角公式などを使う。
s(3A)=s(2A+A)=
c(3A)=c(2A+A)=
(例)「aがπ/2とπの間(cosaが負、sinaが正)でsina=3/5のときの、sin(3a),cos(3a)」は?
cosa=-4/5となるので、sin(3a)=-4sin3a+3sina=-4・27/125+ 3・3/5=-108/125+225/125=117/125
cos(3a)=4cos3a-3cosa=4・(-64/125)- 3・(-4/5)=-256/125+300/125=44/125
(例)cos54°の値は?
p=54とすると5p=270で、270 -2p=3pから、「cos(270 - 2p)=-sin(2p)=cos3p」がなりたつ。
cos54°=c, sin54°=sとおくと、c,sともに正。-sin(2p)=-2sc。cos3p=4c³ー3cだから、
-2sc=4c³-3cの両辺を,cが正だからcで割り、c2=1-s2で、-2s-4(1-s²)+3=0。4s²-2s-1=0。
s=、c=
(例)cos36°の値は?
p=36とすると、5p=180。180- 2p=3p。sin3p=sin(180-2p)=sin2p。
cos36°=c, sin36°=sとおくと、c,sともに正。sin(2p)=2sc。sin3p=-4s³+3sだから、
2sc=-4s³+3sの両辺を,sが正だからsで割り、s2=1-c2で、2c+4(1-c²)-3=0。4c²-2c-1=0。
c=、s=
ちなみに、36+54=90だから、cos36°=sin54°
<4倍角>
c(4A)=
s(4A)=
(理由)
c(4A)=c(2A+2A)=2c(2A)²-1=2(2c²-1)²-1=8c⁴-8c²+1
s(4A)=c(2A+2A)=2s(2A)c(2A)=2・2sc・(1-2s²)=4sc-8s³c
<5倍角>
c(5A)=
s(5A)=
(理由)
c(3A+2A)=c3Ac2A-s3As2A=
=
=
=
s(3A+2A)=s3Ac2A+c3As2A=
=