Cosinus hyperbolicus
II. Mathematische Grundlagen
Cosinus hyperbolicus und Sinus hyperbolicus
Für die mathematische Beschreibung von Kettenlinien wird die Funktion Cosinus hyperbolicus benötigt.
Auf dieser Seite werden diese Funktion und einige ihrer Eigenschaften vorgestellt.
Die Anwendung der Funktion erfolgt im nächsten Kapitel.
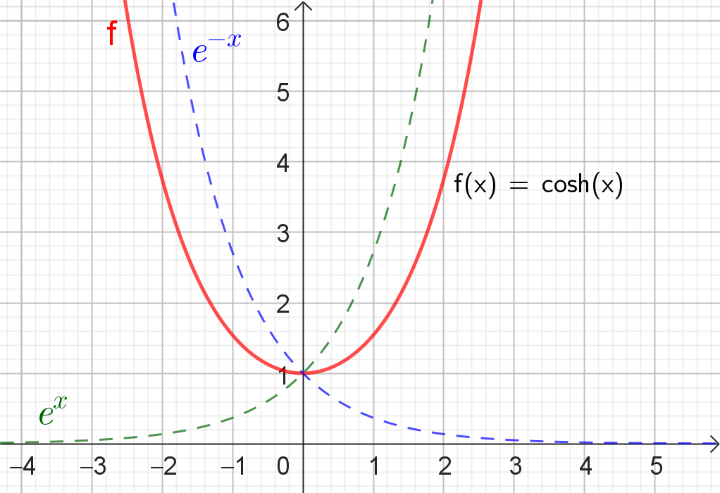
Definition
Die Funktion heißt Cosinus hyperbolicus.
Eigenschaften
Die Funktion ist aufgrund der Definition symmetrisch zur y-Achse.
Ihr Graph ist einer Parabel ähnlich, lässt sich aber nicht exakt durch eine Parabel überdecken.
Der Definitionsbereich ist .
Der Wertebereich ist .
Ableitungen
Aus der Definition ergibt sich mithilfe der Faktor-, Summen- und Kettenregel
Definition
Die Funktion heißt Sinus hyperbolicus.
Vergleich der hyperbolischen Funktionen mit der gewöhnlichen trigonometrischen Sinus- und Kosinusfunktion
Ableitungen
Beziehungen
Exemplarischer Beweis für (I):
Führt man und auf die Definition mit Funktionen zurück, sind die Beweise für die Beziehungen zwischen den hyperbolischen Funktionen alle sehr einfach.