Παράγωγος και κυρτότητα
Οδηγίες
Στη δραστηριότητα δίνεται μία προεπιλεγμένη συνάρτηση f με πεδίο ορισμού το R, ένα σημείο
της Α(x0 , f(x0)), το οποίο μπορείς να μεταβάλεις με τον αντίστοιχο δρομέα x0 και η εφαπτομένη τής
γραφικής της παράστασης σε αυτό.
Με το κουτί «κλίση εφαπτομένης» εμφανίζεις την κλίση της εφαπτομένης στο x0 δηλαδή την παράγωγο f΄(x0) της f στο x0.
Με το κουτί «γραφική παράσταση f΄» εμφανίζεις σε κάθε περίπτωση τη γραφική παράσταση τής παραγώγου τής f.
Με το κουτί «Δεύτερη παράγωγος f΄΄» μπορείς να εμφανίσεις τη γραφική παράσταση της δεύτερης παραγώγου της f.
Σύνδεση της (πρώτης και δεύτερης) παραγώγου μίας συνάρτησης με την κυρτότητά της.
1. Εμφάνισε την κλίση της εφαπτομένης και πειραματίσου μεταβάλλοντας το σημείο Α μέσω του
αντίστοιχου δρομέα.
Παρατήρησε σε κάθε θέση x0 την κλίση της εφαπτομένης ή με άλλα λόγια την παράγωγο f΄(x0).
Εναλλακτικά, με το κουμπί «Κίνηση Α» μπορείς να αφήσεις την εφαρμογή να μεταβάλλει το Α
και εσύ να παρατηρείς πώς μεταβάλλεται η κλίση της εφαπτομένης στα διαστήματα που η f είναι
είτε κοίλη είτε κυρτή.
Με το δρομέα «speed» μπορείς να ρυθμίσεις την ταχύτητα κίνησης του σημείου Α.
Αφού κάνεις τις παρατηρήσεις σου (μπορείς να εμφανίσεις και τις γραφικές παραστάσεις των f΄ και f΄΄ για επαλήθευση), συμπλήρωσε τον ακόλουθο πίνακα:

2. Επίλεξε το κουτί «Κυρτότητα – Σημεία καμπής» και απάντησε στα ερωτήματα της εφαρμογής.
Όταν συμπληρώνεις μία σωστή απάντηση, το αντίστοιχο πλαίσιο γίνεται πράσινο.
Αντίθετα, σε μία λάθος απάντηση γίνεται κόκκινο.
3. Όταν ολοκληρώσεις με την πρώτη συνάρτηση, επίλεξε το κουτί «Επιλογή τύπου» και κάνε κλικ στο
κουμπί «Συνάρτηση 2» για να επιλέξεις μία νέα συνάρτηση.
Επανάλαβε τη διαδικασία των βημάτων 1 και 2.
Σημείωσε τα συμπεράσματά σου στον ακόλουθο πίνακα.

4. Όταν ολοκληρώσεις με τη δεύτερη συνάρτηση, επίλεξε το κουτί «Επιλογή τύπου» και κάνε κλικ στο
κουμπί «Συνάρτηση 3».
Επανάλαβε τη διαδικασία των βημάτων 1 και 2.
Σημείωσε τα συμπεράσματά σου στον ακόλουθο πίνακα.
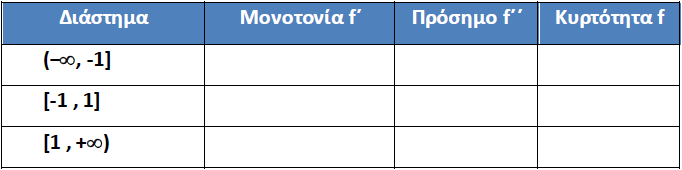
5. Όταν ολοκληρώσεις με την τρίτη συνάρτηση, επίλεξε το κουτί «Επιλογή τύπου» και κάνε κλικ στο
κουμπί «Συνάρτηση 4» και επανάλαβε την προηγούμενη διαδικασία.
Σημείωσε τα συμπεράσματά σου στον ακόλουθο πίνακα.
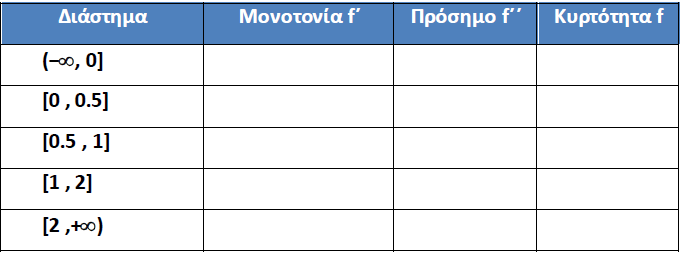
6. Προαιρετική δραστηριότητα:
Επίλεξε το κουμπί «Συνάρτηση5» και μεταβάλλοντας τη θέση του Α παρατήρησε τι συμβαίνει στη
θέση x0 = 3 (κατακόρυφη εφαπτομένη).
(Αλλάζοντας τις τιμές του δρομέα «c», σχηματίζεις μία ασυνεχή συνάρτηση. Επίλεξε στην αρχή c = 1
και μετά μία άλλη τιμή για το c).
Ερώτημα 1
Ποια είναι τα διαστήματα κυρτότητας της f; Έχει η f σημεία καμπής;
Με βάση τις παρατηρήσεις σου, απάντησε στα ακόλουθα ερωτήματα:
Ερώτημα 2
Αν μία συνάρτηση f αλλάζει κυρτότητα στα διαστήματα (α,x0] και [x0,β), τότε είναι βέβαιο ότι το σημείο (x0 , f(x0)) είναι σημείο καμπής της f;
Ερώτημα 3
Αν μία συνάρτηση είναι κυρτή σε ένα διάστημα Δ και δύο φορές παραγωγίσιμη στο εσωτερικό του Δ, τότε είναι βέβαιο ότι f΄΄(x)>0 για κάθε εσωτερικό σημείο x του Δ; Αντίστοιχα, αν μία συνάρτηση είναι κοίλη σε ένα διάστημα Δ και δύο φορές παραγωγίσιμη στο εσωτερικό του Δ, τότε είναι βέβαιο ότι f΄΄(x)<0 για κάθε εσωτερικό σημείο x του Δ;
Ερώτημα 4
Αν μία συνάρτηση f παρουσιάζει στο x0 σημείο καμπής, τότε είναι βέβαιο ότι f΄΄(x0) = 0;
